4. formel¶

Physical equations and useful formulas as quadrature of vector functions, parallel execution, viscosity, compressibility of water, scatteringLengthDensityCalc or sedimentationProfile. Use scipy.constants for physical constants.

Each topic is not enough for a single module, so this is a collection.
All scipy functions can be used. See http://docs.scipy.org/doc/scipy/reference/special.html.
Statistical functions http://docs.scipy.org/doc/scipy/reference/stats.html.

Mass and scattering length of all elements in Elements are taken from :

Mass: http://www.chem.qmul.ac.uk/iupac/AtWt/
Neutron scattering length: http://www.ncnr.nist.gov/resources/n-lengths/list.html

Units converted to amu for mass and nm for scattering length.

4.1. Functions¶

`gauss`(x[, mean, sigma])	Normalized Gaussian function.
`lorentz`(x[, mean, gamma])	Normalized Lorentz function
`voigt`(x[, center, fwhm, lg, asym, amplitude])	Voigt function for peak analysis (normalized).
`lognorm`(x[, mean, sigma])	Lognormal distribution function.
`box`(x[, edges, edgevalue, rtol, atol])	Box function.
`Ea`(z, a[, b])	Mittag-Leffler function for real z and real a,b with 0<a, b<0.
`boseDistribution`(w, temp)	Bose distribution for integer spin particles in non-condensed state (hw>0).
`schulzDistribution`(r, mean, sigma)	Schulz (or Gamma) distribution for polymeric particles/chains.

4.2. Quadrature¶

Routines for efficient integration of parameter dependent vector functions.

`parQuadratureSimpson`(funktion, lowlimit, ...)	Vectorized quadrature over one parameter with weights using the adaptive Simpson rule.
`parQuadratureFixedGauss`(func, lowlimit, ...)	Vectorized definite integral using fixed-order Gaussian quadrature.
`parQuadratureFixedGaussxD`(func, lowlimit, ...)	Vectorized fixed-order Gauss-Legendre quadrature in definite interval in 1,2,3 dimensions.
`parQuadratureAdaptiveGauss`(func, lowlimit, ...)	Vectorized definite integral using fixed-tolerance Gaussian quadrature.
`parQuadratureAdaptiveClenshawCurtis`(func, ...)	Vectorized adaptive multidimensional Clenshaw-Curtis quadrature for 1-3 dimensions.
`parAdaptiveCubature`(func, lowlimit, uplimit, ...)	Vectorized adaptive multidimensional integration (cubature).
`sphereAverage`(funktion[, relError])	Vectorized spherical average of funktion, parallel or non-parallel.
`convolve`(A, B[, mode, normA, normB])	Convolve A and B with proper tracking of the output X axis.

4.3. Distribution of parameters¶

Experimental data might be influenced by multimodal parameters (like multiple sizes) or by one or several parameters distributed around a mean value.

`parDistributedAverage`(funktion, sig, parname)	Vectorized average assuming a single parameter is distributed with width sig.
`multiParDistributedAverage`(funktion, sigs, ...)	Vectorized average assuming multiple parameters are distributed in intervals.
`scatteringFromSizeDistribution`(q, ...[, ...])	Average function assuming one multimodal parameter like bimodal.

4.4. Parallel execution¶

`doForList`(funktion, looplist, args, *kwargs)	Parallel execution of a function in a pool of workers to speed up (multiprocessing).
`shared_create`(ar)	Create shared memory array before sending into pool of workers or usage in doForList .
`shared_recover`(shm_id)	Recover shared memory array inside a function evaluated in a pool of workers.
`shared_close`(shm)	Close and unlink shared memory array.
`sphereAverage`(funktion[, relError])	Vectorized spherical average of funktion, parallel or non-parallel.

4.5. Utilities¶

Helpers for integration and function evaluation in 3D space

`loglist`([mini, maxi, number])	Log like sequence between mini and maxi.
`memoize`(**memkwargs)	A least-recently-used cache decorator to cache expensive function evaluations.
`fibonacciLatticePointsOnSphere`(NN[, r])	Fibonacci lattice points on a sphere with radius r (default r=1)
`randomPointsOnSphere`(NN[, r, skip])	N quasi random points on sphere of radius r based on low-discrepancy sequence.
`randomPointsInCube`(NN[, skip, dim])	N quasi random points in cube of edge 1 based on low-discrepancy sequence.
`haltonSequence`(size, dim[, skip])	Pseudo random numbers from the Halton sequence in interval [0,1].
`xyz2rphitheta`(XYZ[, transpose])	Transformation cartesian coordinates [X,Y,Z] to spherical coordinates [r,phi,theta].
`rphitheta2xyz`(RPT[, transpose])	Transformation spherical coordinates [r,phi,theta] to cartesian coordinates [x,y,z].
`rotationMatrix`(vector, angle)	Create a rotation matrix corresponding to rotation around vector v by a specified angle.
`qEwaldSphere`(q[, wavelength, typ, N])	Points on Ewald sphere with different distributions.
`smooth`(data[, windowlen, window])	Smooth data by convolution with window function or fft/ifft.
`imageHash`(image[, type, hashsize, ...])	Creates image hash of an image to find duplicates or similar images in a fast way using the Hamming difference.

4.6. Centrifugation¶

`sedimentationCoefficient`(M[, partialVol, ...])	Sedimentation coefficient of a sphere in a solvent.
`sedimentationProfile`([t, rm, rb, number, ...])	Concentration profile of sedimenting particles in a centrifuge including bottom equilibrium distribution.
`sedimentationProfileFaxen`([t, rm, rb, ...])	Faxen solution to the Lamm equation of sedimenting particles in centrifuge; no bottom part.

4.7. NMR¶

`DrotfromT12`([t12, Drot, F0, Tm, Ts, T1, T2])	Rotational correlation time from T1/T2 or T1 and T2 from NMR proton relaxation measurement.
`T1overT2`([tr, Drot, F0, T1, T2])	Calculates the T1/T2 from a given rotational correlation time tr or Drot for proton relaxation measurement.

4.8. Material Data¶

`scatteringLengthDensityCalc`(composition[, ...])	Scattering length density of composites and water with inorganic components for xrays and neutrons.
`waterdensity`(composition[, T, units, ...])	Density of water with inorganic substances (salts).
`bufferviscosity`(composition[, T, show])	Viscosity of water with inorganic substances as used in biological buffers.
`dielectricConstant`([material, T, conc, delta])	Dielectric constant of H2O and D2O buffer solutions.
`watercompressibility`([d2ofract, T, units])	Isothermal compressibility of H2O and D2O mixtures.
`cstar`(Rg, Mw)	Overlap concentration \(c^*\) for a polymer.
`molarity`(objekt, c[, total])	Calculates the molarity.
`viscosity`([mat, T])	Viscosity of pure solvents.
`Dtrans`(Rh[, Temp, solvent, visc])	Translational diffusion of a sphere.
`Drot`(Rh[, Temp, solvent, visc])	Rotational diffusion of a sphere.
`perrinFrictionFactor`(p)	Perrin friction factor \(f_P\) for ellipsoids of revolution for tranlational diffusion.
`bicelleRh`(Q, rim, thickness[, k])	Hydrodynamic radius Rh of an ideal bicelle corrected for head group area.

4.9. Constants and Tables¶

`eijk`	Antisymmetric Levi-Civita symbol
`felectron`	electron cross-section
`radiusBohr`	Bohr radius in unit nm
`Elements`	Elements Dictionary with: { symbol : (e- number; mass; neutron coherent scattering length, neutron incoherent scattering length, name)}; units amu for mass and nm for scattering length
`vdwradii`
`xrayFFatomic`	Dict of atomic xray formfactor for elements as dataArray with [q, coherent, incoherent]
`Nscatlength`	Dictionary with neutron scattering length for elements as [b_coherent, b_incoherent].
`aaHydrophobicity`	Hydrophobicity of aminoacids Kyte J, Doolittle RF., J Mol Biol.

Physical equations and useful formulas as quadrature of vector functions, parallel execution, viscosity, compressibility of water, scatteringLengthDensityCalc or sedimentationProfile. Use scipy.constants for physical constants.

Each topic is not enough for a single module, so this is a collection.
All scipy functions can be used. See http://docs.scipy.org/doc/scipy/reference/special.html.
Statistical functions http://docs.scipy.org/doc/scipy/reference/stats.html.

Mass and scattering length of all elements in Elements are taken from :

Mass: http://www.chem.qmul.ac.uk/iupac/AtWt/
Neutron scattering length: http://www.ncnr.nist.gov/resources/n-lengths/list.html

Units converted to amu for mass and nm for scattering length.

jscatter.formel.formel.loglist(mini=0.1, maxi=5, number=100)[source]¶

Log like sequence between mini and maxi.

Parameters:

mini,maxifloat, default 0.1, 5: Start and endpoint.
numberint, default 100: Number of points in sequence.

Returns:

ndarray

jscatter.formel.formel.memoize(**memkwargs)[source]¶

A least-recently-used cache decorator to cache expensive function evaluations.

Memoize caches results and retrieves from cache if same parameters are used again. This can speedup computation in a model if a part is computed with same parameters several times. During fits it may be faster to calc result for a list and take from cache. See also https://docs.python.org/3/library/functools.html cache or lru_cache

Parameters:

functionfunction: Function to evaluate as e.g. f(Q,a,b,c,d)
memkwargsdict: Keyword args with substitute values to cache for later interpolation. Empty for normal caching of a function. E.g. memkwargs={‘Q’:np.r_[0:10:0.1],’t’:np.r_[0:100:5]} caches with these values. The needed values can be interpolated from the returned result. See example below.
maxsizeint, default 128: maximum size of the cache. Last is dropped.

Returns:

function

cached function with new methods

last(i) to retrieve the ith evaluation result in cache (last is i=-1).
clear() to clear the cached results.
hitsmisses counts hits and misses.

Notes

Only keyword arguments for the memoized function are supported!!!! Only one attribute and X are supported for fitting as .interpolate works only for two cached attributes.

Examples

The example uses a model that computes like I(q,n,..)=F(q)*B(t,n,..). F(q) is cheap to calculate B(t,n,..) not. In the following its better to calc the function for a list of q , put it to cache and take in the fit from there. B is only calculated once inside of the function.

Use it like this:

import jscatter as js
import numpy as np

# define some data
TT=js.loglist(0.01,80,30)
QQ=np.r_[0.1:1.5:0.15]
# in the data we have 'q' and 'X'
data=js.dynamic.finiteZimm(t=TT,q=QQ,NN=124,pmax=100,tintern=10,l=0.38,Dcm=0.01,mu=0.5,viscosity=1.001,Temp=300)

# makes a unique list of all X values    -> interpolation is exact for X
# one may also use a smaller list of values and only interpolate
tt=list(set(data.X.flatten));tt.sort()

# define memoized function which will always use the here defined q and t
# use correct values from data for q     -> interpolation is exact for q
memfZ=js.formel.memoize(q=data.q,t=tt)(js.dynamic.finiteZimm)

def fitfunc(Q,Ti,NN,tint,ll,D,mu,viscosity,Temp):
   # use the memoized function as usual (even if given t and q are used from above definition)
   res= memfZ(NN=NN,tintern=tint,l=ll,Dcm=D,pmax=40,mu=mu,viscosity=viscosity,Temp=Temp)
   # interpolate to the here needed q and t (which is X)
   resint=res.interpolate(q=Q,X=Ti,deg=2)[0]
   return resint

# do the fit
data.setlimit(tint=[0.5,40],D=[0,1])
data.makeErrPlot(yscale='l')
NN=20
data.fit(model=fitfunc,
         freepar={'tint':10,'D':0.1,},
         fixpar={'NN':20,'ll':0.38/(NN/124.)**0.5,'mu':0.5,'viscosity':0.001,'Temp':300},
         mapNames={'Ti':'X','Q':'q'},)

Second example

Use memoize as a decorator (@ in front) acting on the following function. This is a shortcut for the above and works in the same way

# define the function to memoize
@js.formel.memoize(Q=np.r_[0:3:0.2],Time=np.r_[0:50:0.5,50:100:5])
def fZ(Q,Time,NN,tintern,ll,Dcm,mu,viscosity,Temp):
    # finiteZimm accepts t and q as array and returns a dataList with different Q and same X=t
    res=js.dynamic.finiteZimm(t=Time,q=Q,NN=NN,pmax=20,tintern=tintern,
                          l=ll,Dcm=Dcm,mu=mu,viscosity=viscosity,Temp=Temp)
    return res

# define the fitfunc
def fitfunc(Q,Ti,NN,tint,ll,D,mu,viscosity,Temp):
   #this is the cached result for the list of Q
   res= fZ(Time=Ti,Q=Q,NN=NN,tintern=tint,ll=ll,Dcm=D,mu=mu,viscosity=viscosity,Temp=Temp)
   # interpolate for the single Q value the cached result has again 'q'
   return res.interpolate(q=Q,X=Ti,deg=2)[0]

# do the fit
data.setlimit(tint=[0.5,40],D=[0,1])
data.makeErrPlot(yscale='l')
data.fit(model=fitfunc,
         freepar={'tint':6,'D':0.1,},
         fixpar={'NN':20,'ll':0.38/(20/124.)**0.5,'mu':0.5,'viscosity':0.001,'Temp':300},
         mapNames={'Ti':'X','Q':'q'})
# the result depends on the interpolation;

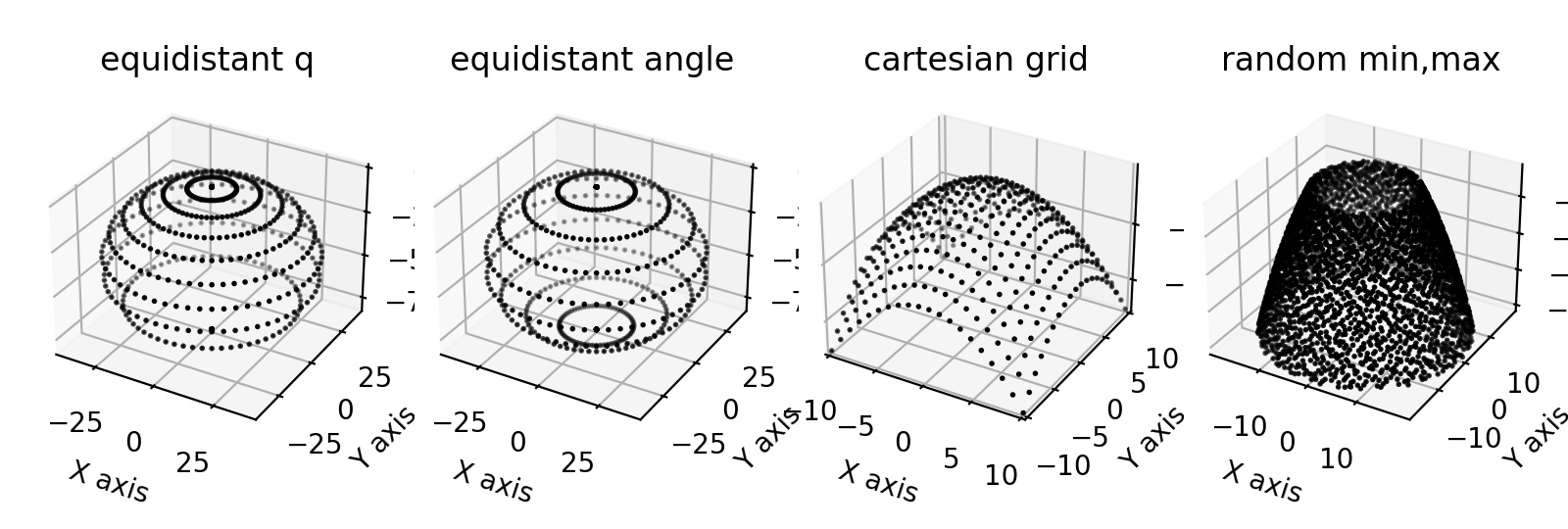
jscatter.formel.formel.qEwaldSphere(q, wavelength=0.15406, typ=None, N=60)[source]¶

Points on Ewald sphere with different distributions.

\(q = \vec{k_s} -\vec{k_i} =4\pi/\lambda sin(\theta/2)\) with \(\vec{k_i} =[0,0,1]\) and \(|\vec{k_i}| =2\pi/\lambda\)

Use rotation matrix to rotate to specific orientations.

Parameters:

qarray,list

Wavevectors units 1/nm

wavelengthfloat

Wavelength of radiation, default X-ray K_a.

Ninteger

Number of points in intervals.

typ‘cart’,’ring’,’random’ default=’ring’

Typ of q value distribution on Ewald sphere.

cart : Cartesian grid between -q_max,q_max with N points (odd to include zero).
ring : Given q values with N-points on rings of equal q.
random : N² random points on Ewald sphere between q_min and q_max.

Returns:

array3xN [x,y,z] coordinates

Examples

import jscatter as js
import numpy as np
fig = js.mpl.figure(figsize=[8, 2.7],dpi=200)
ax1 = fig.add_subplot(1, 4, 1, projection='3d')
ax2 = fig.add_subplot(1, 4, 2, projection='3d')
ax3 = fig.add_subplot(1, 4, 3, projection='3d')
ax4 = fig.add_subplot(1, 4, 4, projection='3d')
q0 = 2 * np.pi / 0.15406  # Ewald sphere radius |kin|

q = np.r_[0.:2*q0:10j]
qe = js.formel.qEwaldSphere(q)
js.mpl.scatter3d(qe[0],qe[1],qe[2],ax=ax1,pointsize=1)
ax1.set_title('equidistant q')

q = 2*q0*np.sin(np.r_[0.:np.pi:10j]/2)
qe = js.formel.qEwaldSphere(q)
js.mpl.scatter3d(qe[0],qe[1],qe[2],ax=ax2,pointsize=1)
ax2.set_title('equidistant angle')

qe = js.formel.qEwaldSphere(q=[10],N=20,typ='cart')
js.mpl.scatter3d(qe[0],qe[1],qe[2],ax=ax3,pointsize=1)
ax3.set_title('cartesian grid')

qe = js.formel.qEwaldSphere(q=[10,0.5*q0],N=60,typ='random')
fig = js.mpl.scatter3d(qe[0],qe[1],qe[2],ax=ax4,pointsize=1)
ax4.set_title('random min,max')
#fig.savefig(js.examples.imagepath+'/qEwaldSphere.jpg')

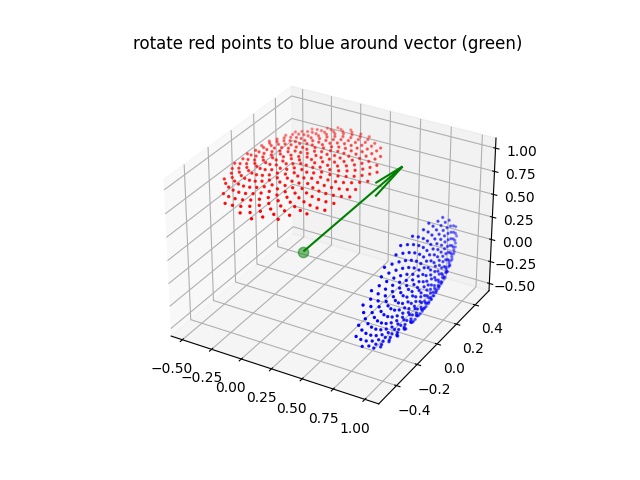
jscatter.formel.formel.rotationMatrix(vector, angle)[source]¶

Create a rotation matrix corresponding to rotation around vector v by a specified angle.

\[R = vv^T + cos(a) (I - vv^T) + sin(a) skew(v)\]

See Notes for scipy rotation matrix.

Parameters:

vectorarray: Rotation around a general vector
anglefloat: Angle in rad

Returns:

array: Rotation matrix

Notes

A convenient way to define more complex rotations is found in scipy.spatial.transform.Rotation . E.g. by Euler angles and returned as rotation matrix

from scipy.spatial.transform import Rotation as Rot
R=Rot.from_euler('YZ',[90,10],1).as_matrix()

References

[1]

https://en.wikipedia.org/wiki/Rotation_matrix#Rotation_matrix_from_axis_and_angle

Examples

Examples show how to use a rotation matrix with vectors.

import jscatter as js
import numpy as np
from matplotlib import pyplot
R=js.formel.rotationMatrix([0,0,1],np.deg2rad(-90))
v=[1,0,0]
# rotated vector
rv=np.dot(R,v)
#
# rotate Fibonacci Grid
qfib=js.formel.fibonacciLatticePointsOnSphere(300,1)
qfib=qfib[qfib[:,2]<np.pi/2,:]                       # select half sphere
qfib[:,2]*=(30/90.)                                  # shrink to cone of 30°
qfx=js.formel.rphitheta2xyz(qfib)                    # transform to cartesian
v = [0,1,0]                                          # rotation vector
R=js.formel.rotationMatrix(v,np.deg2rad(90))        # rotation matrix around v axis
Rfx=np.einsum('ij,kj->ki',R,qfx)                     # do rotation
fig = pyplot.figure()
ax = fig.add_subplot(111, projection='3d')
sc=ax.scatter(qfx[:,0], qfx[:,1], qfx[:,2], s=2, color='r')
sc=ax.scatter(Rfx[:,0], Rfx[:,1], Rfx[:,2], s=2, color='b')
ax.scatter(0,0,0, s=55, color='g',alpha=0.5)
ax.quiver([0],[0],[0],*v,color=['g'])
fig.axes[0].set_title('rotate red points to blue around vector (green)')
pyplot.show(block=False)
# fig.savefig(js.examples.imagepath+'/rotationMatrix.jpg')

jscatter.formel.formel.rphitheta2xyz(RPT, transpose=False)[source]¶

Transformation spherical coordinates [r,phi,theta] to cartesian coordinates [x,y,z].

Parameters:

RPTarray Nx3

Coordinates with [r,phi,theta]

r : float length
phi : float azimuth -pi < phi < pi
theta : float polar angle 0 < theta < pi

transposebool

Transpose RPT before transformation.

Returns:

array Nx3: [x,y,z] coordinates

jscatter.formel.formel.smooth(data, windowlen=7, window='flat')[source]¶

Smooth data by convolution with window function or fft/ifft.

Smoothing based on position ignoring information on .X.

Parameters:

dataarray, dataArray

Data to smooth. If is dataArray the .Y is smoothed and returned.

windowlenint, default = 7

The length/size of the smoothing window; should be an odd integer. Smaller 3 returns unchanged data. For ‘fourier’ the high frequency cutoff is 2*size_data/windowlen.

window‘hann’, ‘hamming’, ‘bartlett’, ‘blackman’,’gaussian’,’fourier’,’flattop’ default =’flat’

Type of window/smoothing.

‘flat’ will produce a moving average smoothing.
‘gaussian’ normalized Gaussian window with sigma=windowlen/7.
‘fourier’ cuts high frequencies above cutoff frequency between rfft and irfft.

Returns:

array (only the smoothed array)

Notes

‘hann’, ‘hamming’, ‘bartlett’, ‘blackman’,’gaussian’, ‘flat’ :

These methods convolve a scaled window function with the signal. The signal is prepared by introducing reflected copies of the signal (with the window size) at both ends so that transient parts are minimized in the beginning and end part of the output signal. Adapted from SciPy/Cookbook.

See https://docs.scipy.org/doc/scipy-1.11.0/reference/generated/scipy.signal.get_window.html#scipy.signal.get_window

fourier :

The real valued signal is mirrored at left side, Fourier transformed, the high frequencies are cut and the signal is back transformed. This is the simplest form as a hard cutoff frequency is used (ideal low pass filter) and may be improved using a specific window function in frequency domain.

rft = np.fft.rfft(np.r_[data[::-1],data])
rft[int(2*len(data)/windowlen):] = 0
smoothed = np.fft.irfft(rft)

Examples

Usage:

import jscatter as js
import numpy as np
t=np.r_[-5:5:0.01]
data=np.sin(t)+np.random.randn(len(t))*0.1
y=js.formel.smooth(data)  # 1d array
#
# smooth dataArray and replace .Y values.
data2=js.dA(np.vstack([t,data]))
data2.Y=js.formel.smooth(data2, windowlen=40, window='gaussian')

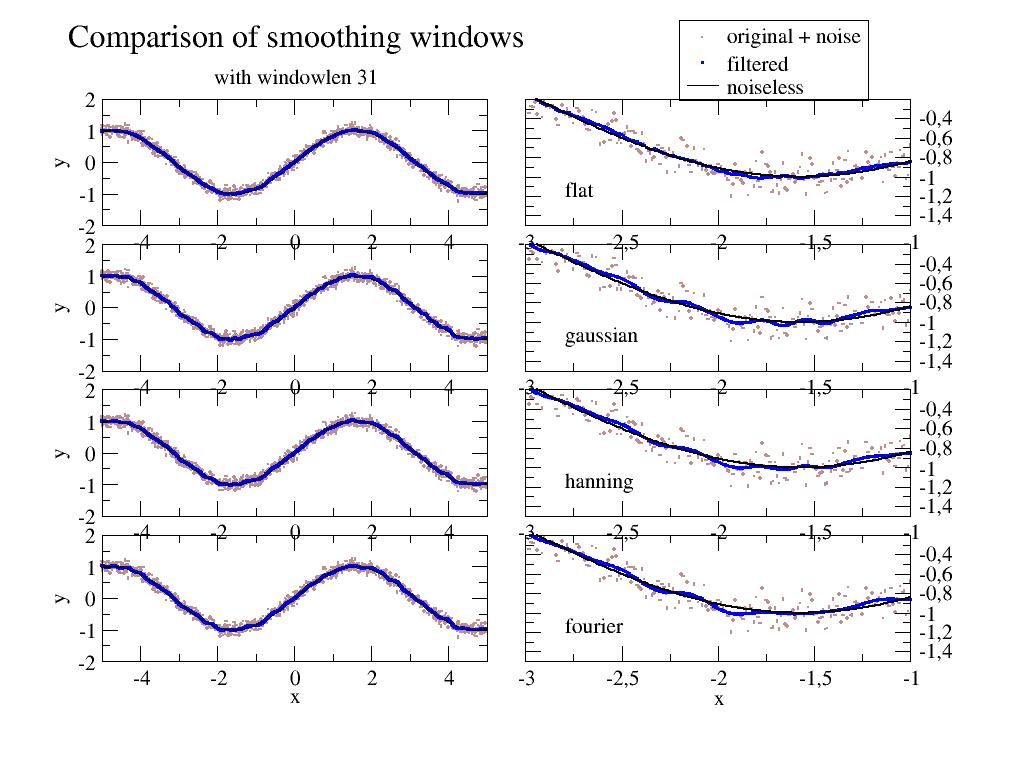
Comparison of some filters:

import jscatter as js
import numpy as np
t=np.r_[-5:5:0.01]
data=js.dA(np.vstack([t,np.sin(t)+np.random.randn(len(t))*0.1]))
p=js.grace()
p.multi(4,2)
windowlen=31
for i,window in enumerate(['flat','gaussian','hann','fourier']):
    p[2*i].plot(data,sy=[1,0.1,6],le='original + noise')
    p[2*i].plot(t,js.formel.smooth(data,windowlen,window),sy=[2,0.1,4],le='filtered')
    p[2*i].plot(t,np.sin(t),li=[1,0.5,1],sy=0,le='noiseless')
    p[2*i+1].plot(data,sy=[1,0.1,6],le='original noise')
    p[2*i+1].plot(t,js.formel.smooth(data,windowlen,window),sy=[2,0.1,4],le=window)
    p[2*i+1].plot(t,np.sin(t),li=[1,2,1],sy=0,le='noiseless')
    p[2*i+1].text(window,x=-2.8,y=-1.2)
    p[2*i+1].xaxis(min=-3,max=-1,)
    p[2*i+1].yaxis(min=-1.5,max=-0.2,ticklabel=[None,None,None,'opposite'])
    p[2*i].yaxis(label='y')
p[0].legend(x=10,y=4.5)
p[6].xaxis(label='x')
p[7].xaxis(label='x')
p[0].title(f'Comparison of smoothing windows')
p[0].subtitle(f'with windowlen {windowlen}')
#p.save(js.examples.imagepath+'/smooth.jpg')

jscatter.formel.formel.xyz2rphitheta(XYZ, transpose=False)[source]¶

Transformation cartesian coordinates [X,Y,Z] to spherical coordinates [r,phi,theta].

Parameters:

XYZarray Nx3: Coordinates with [x,y,z] ( XYZ.shape[1]==3).
transposebool: Transpose XYZ before transformation.

Returns:

array Nx3

Coordinates with [r,phi,theta]

phi : float azimuth -pi < phi < pi
theta : float polar angle 0 < theta < pi
r : float length

Examples

Single coordinates

js.formel.xyz2rphitheta([1,0,0])

Transform Fibonacci lattice on sphere to xyz coordinates

rpc=js.formel.randomPointsInCube(10)
js.formel.xyz2rphitheta(rpc)

Tranformation 2D X,Y plane coordinates to r,phi coordinates (Z=0)

rp=js.formel.xyz2rphitheta([data.X,data.Z,abs(data.X*0)],transpose=True) )[:,:2]

Physical equations and useful formulas as quadrature of vector functions, parallel execution, viscosity, compressibility of water, scatteringLengthDensityCalc or sedimentationProfile. Use scipy.constants for physical constants.

Each topic is not enough for a single module, so this is a collection.
All scipy functions can be used. See http://docs.scipy.org/doc/scipy/reference/special.html.
Statistical functions http://docs.scipy.org/doc/scipy/reference/stats.html.

Mass and scattering length of all elements in Elements are taken from :

Mass: http://www.chem.qmul.ac.uk/iupac/AtWt/
Neutron scattering length: http://www.ncnr.nist.gov/resources/n-lengths/list.html

Units converted to amu for mass and nm for scattering length.

jscatter.formel.physics.Drot(Rh, Temp=293.15, solvent='h2o', visc=None)[source]¶

Rotational diffusion of a sphere.

\[D = \frac{k_\text{B} T}{8 \pi \eta R_h^3}\]

Parameters:

Rhfloat: Hydrodynamic radius in nm.
Tempfloat: Temperature in K.
solventfloat: Solvent type as in viscosity; used if visc==None.
viscfloat: Viscosity in Pas => H2O ~ 0.001 Pa*s =1 cPoise. If visc=None the solvent viscosity is calculated from function viscosity(solvent ,temp) with solvent e.g.’h2o’.

Returns:

float: Rotational diffusion coefficient in 1/ns.

jscatter.formel.physics.DrotfromT12(t12=None, Drot=None, F0=20000000.0, Tm=None, Ts=None, T1=None, T2=None)[source]¶

Rotational correlation time from T1/T2 or T1 and T2 from NMR proton relaxation measurement.

Allows to rescale by temperature and viscosity.

Parameters:

t12float: T1/T2 from NMR with unit seconds
Drotfloat: !=None means output Drot instead of rotational correlation time.
F0float: Resonance frequency of NMR instrument. For Hydrogen F0=20 MHz => w0=F0*2*np.pi
Tm: float: Temperature of measurement in K.
Tsfloat: Temperature needed for Drot -> rescaled by visc(T)/T.
T1float: NMR T1 result in s
T2float: NMR T2 result in s to calc t12 directly remeber if the sequence has a factor of 2

Returns:

float: Correlation time or Drot

Notes

See T1overT2

jscatter.formel.physics.Dtrans(Rh, Temp=293.15, solvent='h2o', visc=None)[source]¶

Translational diffusion of a sphere.

\[D = \frac{k_\text{B} T}{6 \pi \eta R_h}\]

Parameters:

Rhfloat: Hydrodynamic radius in nm.
Tempfloat: Temperature T in K.
solventfloat: Solvent type as in viscosity; used if visc==None.
viscfloat: Viscosity \(\eta\) in Pas => H2O ~ 0.001 Pas =1 cPoise. If visc=None the solvent viscosity is calculated from function viscosity(solvent ,temp) with solvent e.g.’h2o’ (see viscosity).

Returns:

Dfloat: Translational diffusion coefficient : float in nm^2/ns.

jscatter.formel.physics.T1overT2(tr=None, Drot=None, F0=20000000.0, T1=None, T2=None)[source]¶

Calculates the T1/T2 from a given rotational correlation time tr or Drot for proton relaxation measurement.

tr=1/(6*D_rot) with rotational diffusion D_rot and correlation time tr.

Parameters:

trfloat: Rotational correlation time.
Drotfloat: If given tr is calculated from Drot.
F0float: NMR frequency e.g. F0=20e6 Hz=> w0=F0*2*np.pi is for Bruker Minispec with B0=0.47 Tesla
T1float: NMR T1 result in s
T2float: NMR T2 resilt in s to calc t12 directly

Returns:

float: T1/T2

Notes

\(J(\omega)=\tau/(1+\omega^2\tau^2)\)

\(T1^{-1}=\frac{\sigma}{3} (2J(\omega_0)+8J(2\omega_0))\)

\(T2^{-1}=\frac{\sigma}{3} (3J(0)+ 5J(\omega_0)+2J(2\omega_0))\)

\(tr=T1/T2\)

References

[1]

Intermolecular electrostatic interactions and Brownian tumbling in protein solutions. Krushelnitsky A Physical chemistry chemical physics 8, 2117-28 (2006)

[2]

The principle of nuclear magnetism A. Abragam Claredon Press, Oxford,1961

jscatter.formel.physics.bicelleRh(Q, rim, thickness, k=1.6666666666666667)[source]¶

Hydrodynamic radius Rh of an ideal bicelle corrected for head group area.

Parameters:

Qfloat: Ratio of lipid composition
rimfloat: Radius of the rim.
thicknessfloat: Thickness of the bicelle planar region
kfloat: Head group area ratio. like 1/0.6 for rim DHCP 1nm² and planar DMPC 0.6nm²

Returns:

[Rhfloat, R: float, R + rim]
R radius of the planar region

Notes

Bicelle radius R with lipid area correction factor k [1] :

\[R = \frac{1}{2} k r Q [\pi +(\pi^2 + 8k/Q)^{1/2}]\]

Rh of a (rectangular) disk with radius \(r^{\prime}\) and thickness t (same for a longer rod t>r’) [2] :

\[R_h = \frac{3}{2}r^{\prime} \Big[[1+(\frac{t}{2r^{\prime}})^2]^{1/2}-\frac{t}{2r^{\prime}} + \frac{2r^{\prime}}{t} ln\big(\frac{t}{2r^{\prime}} + [1+(\frac{t}{2r^{\prime}})^2]^{1/2}\big)\Big]^{-1}\]

with \(r^{\prime} = R+r\) outer radius, rim radius \(r\), lipid ratio \(Q\), thickness t

It should be noted that in the references reporting this equation the hydrodynamic radius from DLS measurements is reported to be concentration dependent. This results from ignoring the structure factor effects (see hydrodynamicFunct()) and leads to misinterpretation of the disc radius.

References

[1]

Structural Evaluation of Phospholipid Bicelles for Solution-State Studies of Membrane-Associated Biomolecules Glover, et al.Biophysical Journal 81(4), 2163–2171 (2001)

[2]

Quasielastic Light-Scattering Studies of Aqueous Biliary Lipid Systems. Mixed Micelle Formation in Bile Salt-Lecithin Solutions Mazer et al.Biochemistry 19, 601–615 (1980), https://doi.org/10.1021/bi00545a001

jscatter.formel.physics.bufferviscosity(composition, T=293.15, show=False)[source]¶

Viscosity of water with inorganic substances as used in biological buffers.

Solvent with composition of H2O and D2O and additional components at temperature T. Ternary solutions allowed. Units are mol; 1l h2o = 55.50843 mol Based on data from ULTRASCAN3 [1] supplemented by the viscosity of H2O/D2O mixtures for conc=0.

Parameters:

compositionlist of compositional strings: Compositional strings of chemical name as ‘float’+’name’ First float is content in Mol followed by component name as ‘h2o’ or ‘d2o’ light and heavy water were mixed with prepended fractions.

[‘1.5urea’,’0.1sodiumchloride’,’2h2o’,’1d2o’] for 1.5 M urea + 100 mM NaCl in a 2:1 mixture of h2o/d2o. By default ‘1h2o’ is assumed.
Tfloat, default 293.15: Temperature in K
showbool, default False: Show composition and validity range of components and result in mPas.

Returns:

float: Viscosity in Pa*s

Notes

Viscosities of H2O/D2O mixtures mix by linear interpolation between concentrations (accuracy 0.2%) [2].
The change in viscosity due to components is added based on data from Ultrascan3 [1].
Multicomponent mixtures are composed of binary mixtures.
“Glycerol%” is in unit “%weight/weight” for range=”0-32%, here the unit is changed to weight% insthead of M.
Propanol1, Propanol2 are 1-Propanol, 2-Propanol

References

[1] (1,2)

http://www.ultrascan3.uthscsa.edu/

[2]

Viscosity of light and heavy water and their mixtures Kestin Imaishi Nott Nieuwoudt Sengers, Physica A: Statistical Mechanics and its Applications 134(1):38-58

[3]

Thermal Offset Viscosities of Liquid H2O, D2O, and T2O C. H. Cho, J. Urquidi, S. Singh, and G. Wilse Robinson J. Phys. Chem. B 1999, 103, 1991-1994

availible components:

h2o1 d2o1
     aceticacid                acetone                   ammoniumacetate          
 ammoniumchloride          ammoniumhydroxide         ammoniumsulfate          
 bariumchloride            cadmiumchloride           cadmiumsulfate           
 calciumchloride           cesiumchloride            citricacid               
 cobaltouschloride         creatinine                cupricsulfate            
 edtadisodium              ethanol                   ethyleneglycol           
 ferricchloride            formicacid                fructose                 
 glucose                   glycerol                  glycerol%                
 guanidinehydrochloride    hydrochloricacid          inulin                   
 lacticacid                lactose                   lanthanumnitrate         
 leadnitrate               lithiumchloride           magnesiumchloride        
 magnesiumsulfate          maltose                   manganoussulfate         
 mannitol                  methanol                  nickelsulfate            
 nitricacid                oxalicacid                phosphoricacid           
 potassiumbicarbonate      potassiumbiphthalate      potassiumbromide         
 potassiumcarbonate        potassiumchloride         potassiumchromate        
 potassiumdichromate       potassiumferricyanide     potassiumferrocyanide    
 potassiumhydroxide        potassiumiodide           potassiumnitrate         
 potassiumoxalate          potassiumpermanganate     potassiumphosphate,dibasic
 potassiumphosphate,monobasic potassiumsulfate          potassiumthiocyanate     
 procainehydrochloride     propanol1                 propanol2                
 propyleneglycol           silvernitrate             sodiumacetate            
 sodiumbicarbonate         sodiumbromide             sodiumcarbonate          
 sodiumchloride            sodiumcitrate             sodiumdiatrizoate        
 sodiumdichromate          sodiumferrocyanide        sodiumhydroxide          
 sodiummolybdate           sodiumphosphate,dibasic   sodiumphosphate,monobasic
 sodiumphosphate,tribasic  sodiumsulfate             sodiumtartrate           
 sodiumthiocyanate         sodiumthiosulfate         sodiumtungstate          
 strontiumchloride         sucrose                   sulfuricacid             
 tartaricacid              tetracainehydrochloride   trichloroaceticacid      
 trifluoroethanol          tris(hydroxymethyl)aminomethane urea                     
 zincsulfate              

jscatter.formel.physics.cstar(Rg, Mw)[source]¶

Overlap concentration \(c^*\) for a polymer.

Equation 3 in [1] (Cotton) defines \(c^*\) as overlap concentration of space filling volumes corresponding to a cube or sphere with edge/radius equal to \(R_g\)

\[\frac{ M_w }{ N_A R_g^3} \approx c^* \approx \frac{3M_w}{4N_A \pi R_g^3}\]

while equ. 4 uses cubes with \(2R_g\) (Graessley) \(c^* = \frac{ M_w }{ N_A 2R_g^3 }\) .

Parameters:

Rgfloat in nm: radius of gyration
Mwfloat: molecular weight

Returns:

floatx3: Concentration limits [cube_rg, sphere_rg, cube_2rg] in units g/l.

References

[1]

Overlap concentration of macromolecules in solution Ying, Q. & Chu, B. Macromolecules 20, 362–366 (1987)

jscatter.formel.physics.dielectricConstant(material='d2o', T=293.15, conc=0, delta=5.5)[source]¶

Dielectric constant of H2O and D2O buffer solutions.

Dielectric constant \(\epsilon\) of H2O and D2O (error +- 0.02) with added buffer salts.

\[\epsilon (c)=\epsilon (c=0)+2c\: delta\; for\; c<2M\]

Parameters:

materialstring ‘d2o’ (default) or ‘h2o’: Material ‘d2o’ (default) or ‘h2o’
Tfloat: Temperature in °C
concfloat: Salt concentration in mol/l.
deltafloat: Total excess polarisation dependent on the salt and presumably on the temperature!

Returns:

float: Dielectric constant

Notes

Salt	delta(+-1)	deltalambda (not used here)
HCl	-10	0
LiCl	7	-3.5
NaCl	5.5	`-4` default
KCl	5	-4
RbCl	5	-4.5
NaF	6	-4
KF	6.5	-3.5
NaI	-7.5	-9.5
KI	-8	-9.5
MgCI,	-15	-6
BaCl2	-14	-8.5
LaCI.	-22	-13.5
NaOH	-10.5	-3
Na2SO.	-11	-9.5

References

[1]

Dielectric Constant of Water from 0 to 100 C. G . Malmberg and A. A. Maryott Journal of Research of the National Bureau of Standards, 56,1 ,369131-56–1 (1956) Research Paper 2641

[2]

Dielectric Constant of Deuterium Oxide C.G Malmberg, Journal of Research of National Bureau of Standards, Vol 60 No 6, (1958) 2874 http://nvlpubs.nist.gov/nistpubs/jres/60/jresv60n6p609_A1b.pdf

[3]

Dielectric Properties of Aqueous Ionic Solutions. Parts I and II Hasted et al. J Chem Phys 16 (1948) 1 http://link.aip.org/link/doi/10.1063/1.1746645

jscatter.formel.physics.molarity(objekt, c, total=None)[source]¶

Calculates the molarity.

Parameters:

objektobject,float: Objekt with method .mass() or molecular weight in Da.
cfloat: Concentration in g/ml -> mass/Volume
totalfloat, default None: Total volume in milliliter [ml] Concentration is calculated by c[g]/total[ml] if given.

Returns:

float: molarity in mol/liter (= mol/1000cm^3)

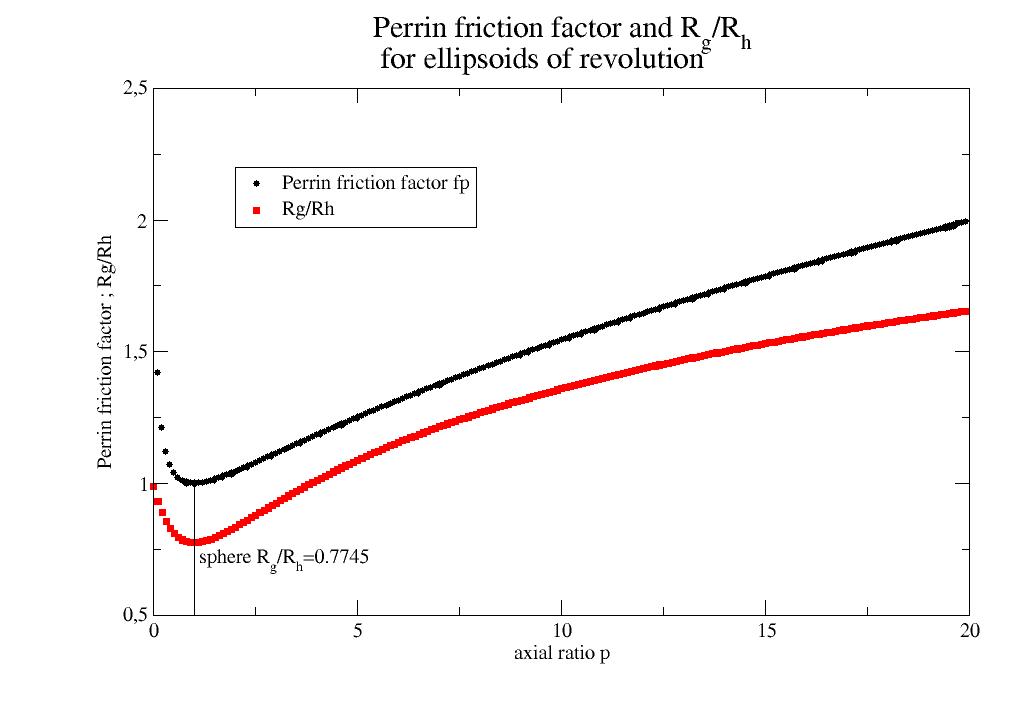
jscatter.formel.physics.perrinFrictionFactor(p)[source]¶

Perrin friction factor \(f_P\) for ellipsoids of revolution for tranlational diffusion.

Parameters:

parray of float

Axial ratio p=a/b with semiaxes a (along the axis of revolution) and b(=c) (equatorial semiaxis).

p>1 for prolate ellipsoids (cigar like)
0<p<1 for oblate ellipsoids (disc like)

Returns:

Perrin friction factorarray

Notes

Translational diffusion of a sphere is \(D_t=kT/f_{sphere}\) with the sphere friction \(f_{sphere}=6\pi \eta R_h\) of a sphere with hydrodynamic radius \(R_h\).

For aspherical bodies like ellipsoids or proteins \(R_h\) is an equivalent sphere radius showing the same \(D_t\) . This was calculated by Perrin [2] for ellipsoids of revolution with semiaxes a,b(=c)

\[f_{sphere} = f_{sphere,R_h} f_P\]

with the axial ratio \(p=a/b\) (see [1] )

\[ \begin{align}\begin{aligned}f_P &= p^{2/3} \frac{\sqrt{1-1/p^2}}{ln((1+\sqrt{1-1/p^2})p)} &\text{ for p>1 prolate }\\&= p^{2/3} \frac{\sqrt{1/p^2-1}}{arctan(\sqrt{1/p^2-1})} &\text{ for p<1 oblate}\end{aligned}\end{align} \]

The prefactor \(p^{2/3}\) results from the conversion of the \(R_h\) as a sphere with equivalent volume of the ellipsoid \(R_h=(3V_{ellipsoid}/4\pi)^{1/3}\) and \(V_{ellipsoid}=\frac{4\pi}{3} ab^2 = \frac{4pi}{3} a^3/p^2\) .

References

[1]

On the hydrodynamic analysis of macromolecular conformation. Harding, S. E. Biophysical Chemistry, 55, 69–93 (1995) https://doi.org/10.1016/0301-4622(94)00143-8

[2]

Mouvement brownien d’un ellipsoide-I. Dispersion diélectrique pour des molécules ellipsoidales. F Perrin J Phys-Paris 5, 497–511 (1934).

Examples

Calculation \(R_g/R_h\) for ellipsoids for simple shape analysis by comparing \(R_h\) from DLS and \(R_g\) from static light scattering or SAXS.

import jscatter as js
import numpy as np

pp = np.r_[0.01:20:0.1]
fp = js.formel.perrinFrictionFactor(pp)

p= js.grace()
p.plot(pp, fp , le='Perrin friction factor fp')

Rh = lambda p: js.formel.perrinFrictionFactor(p) * (1/p**2)**(1/3)
Rg = lambda p: (1/5*(1+2/pp**2))**0.5

p.plot(pp, Rg(pp) / Rh(pp) , le='Rg/Rh' )
p.plot([1,1],[0.5,1],li=1,sy=0)
p.xaxis(label='axial ratio p')
p.yaxis(label='Perrin friction factor ; Rg/Rh',min=0.5,max=2.5)
p.legend(x=2,y=2.2)
p.text(r'sphere R\sg\N/R\sh\N=0.7745',x=1.1,y=0.7)
p.subtitle(r'Perrin friction factor and R\sg\N/R\sh\N \n for ellipsoids of revolution',size=1.5)
# p.save(js.examples.imagepath+'/PerrinFrictionFactor.jpg')

jscatter.formel.physics.scatteringLengthDensityCalc(composition, density=None, T=293, units='mol', mode='all')[source]¶

Scattering length density of composites and water with inorganic components for xrays and neutrons.

Parameters:

compositionlist of concentration + chemical formula

A string with chemical formula as letter + number and prepended concentration in mol or mmol. E.g. ‘0.1C3H8O3’ or ‘0.1C3H1D7O3’ for glycerol and deuterated glycerol (‘D’ for deuterium).

For single atoms append 1 to avoid confusion. Fractional numbers allowed, but think of meaning (Isotope mass fraction??)

For compositions use a list of strings preceded by mass fraction or concentration in mol of component. This will be normalized to total amount

Examples:

[‘4.5H2O1’,’0.5D2O1’] mixture of 10% heavy and 90% light water.
[‘1.0h2o’,’0.1c3h8o3’] for 10% mass glycerol added to 100% h2o with units=’mass’
[‘55000H2O1’,’50Na3P1O4’,’137Na1Cl1’] for a 137mMol NaCl +50mMol phophate H2O buffer (1l is 55000 mM H2O)
[‘1Au1’] gold with density 19.302 g/ml

Remember to adjust density.

densityfloat, default=None

Density in g/cm**3 = g/ml.

If not given function waterdensity is tried to calculate the solution density with inorganic components. In this case ‘h2o1’ and/or ‘d2o1’ need to be in composition.
Density can be measure by weighting a volume from pipette (lower accuracy) or densiometry (higher accuracy).
Estimate for deuterated compounds from protonated density according to additional D. Mass change is given with mode=’all’.

units‘mol’

Anything except ‘mol’ prepended unit is mass fraction (default). ‘mol’ prepended units is mol and mass fraction is calculated as mass=[mol]*mass_of_molecule e.g. 1l Water with 123mmol NaCl [‘55.5H2O1’,’0.123Na1Cl1’]

mode

‘xsld’ xray scattering length density in nm**-2
‘edensity’ electron density in e/nm**3
‘ncohsld’ coherent scattering length density in nm**-2
‘incsld’ incoherent scattering length density in nm**-2
‘num’ number density of components in 1/nm**3
‘all’ [xsld, edensity, ncohsld, incsld,
masses, masses full protonated, masses full deuterated, d2o/h2o mass fraction, d2o/h2o mol fraction]

= ‘all2’ [xsld, edensity, ncohsld, incsld,: masses, masses full protonated, masses full deuterated, d2o/h2o number fraction, number densities in 1/nm³, density in g/cm³]

Tfloat, default=293

Temperature in °K

Returns:

float, list: sld corresponding to mode

Notes

edensity=be*massdensity/weightpermol*sum_atoms(numberofatomi*chargeofatomi)
be = scattering length electron =µ0*e**2/4/pi/m=2.8179403267e-6 nm
masses, masses full protonated, masses full deuterated for each chemical in composition.
In mode ‘all’ the masses can be used to calc the deuterated density if same volume is assumed. e.g. fulldeuterated_density=protonated_density/massfullprotonated*massfulldeuterated

For density reference of H2O/D2O see waterdensity.

Examples

# 5% D2O in H2O with 10% mass NaCl
js.formel.scatteringLengthDensityCalc(['9.5H2O1','0.5D2O1','1Na1Cl1'],units='mass')
# protein NaPi buffer in D2O prevalue in mmol; 55507 mmol H2O is 1 liter.
# because of the different density the sum of number density is not 55.507 mol but 55.191 mol.
js.formel.scatteringLengthDensityCalc(['55507D2O1','50Na3P1O4','137Na1Cl1'])
# silica
js.formel.scatteringLengthDensityCalc('1Si1O2',density=2.65)
# gold
js.formel.scatteringLengthDensityCalc(['1Au1'],density=19.32)
# PEG1000
js.formel.scatteringLengthDensityCalc(['1C44H88O23'],density=1.21)

jscatter.formel.physics.sedimentationCoefficient(M, partialVol=None, density=None, visc=None)[source]¶

Sedimentation coefficient of a sphere in a solvent.

\(S = M (1-\nu \rho)/(N_A 6\pi \eta R)\) with \(V = 4/3\pi R^3 = \nu M\)

Parameters:

Mfloat: Mass of the sphere or protein in units Da.
partialVolfloat: Partial specific volume \(\nu\) of the particle in units ml/g = l/kg. Default is 0.73 ml/g for proteins.
densityfloat: Density \(\rho\) of the solvent in units g/ml=kg/l. Default is H2O at 293.15K
viscfloat: Solvent viscosity \(\eta\) in Pas. Default H2O at 293.15K

Returns:

float: Sedimentation coefficient in units Svedberg (1S = 1e-13 sec )

jscatter.formel.physics.sedimentationProfile(t=1000.0, rm=48, rb=85, number=100, rlist=None, c0=0.01, S=None, Dt=None, omega=246, Rh=10, temp=293, densitydif=0.37, visc='h2o')[source]¶

Concentration profile of sedimenting particles in a centrifuge including bottom equilibrium distribution.

Approximate solution to the Lamm equation including the bottom equilibrium distribution which is not included in the Faxen solution. This calculates equ. 28 in [1]. Results in particle concentration profile between rm and rb for time t with a equal distribution at the start.

Parameters:

tfloat or list: Time after centrifugation start in seconds. If list, a dataList for all times is returned.
rmfloat: Axial position of meniscus in mm.
rbfloat: Axial position of bottom in mm.
numberint: Number of points between rm and rb to calculate.
rlistlist of float: Explicit list of positions where to calculate e.g.to zoom bottom.
c0float: Initial concentration in cell; just a scaling factor.
Sfloat: Sedimentation coefficient in units Svedberg; 82 S is r=10 nm protein in H2O at T=20C.
Dtfloat: Translational diffusion coefficient in m**2/s; 1.99e-11 is r=10 nm particle.
omegafloat: Radial velocity rounds per second; 14760rpm = 246 rps = 1545 rad/s is 20800g in centrifuge fresco 21.
Rhfloat: Hydrodynamic radius in nm ; if given the Dt and s are calculated from this.
densitydiffloat: Density difference between solvent and particle in g/ml; Protein in ‘h2o’ => 1.37-1.= 0.37 g/cm**3.
viscfloat, ‘h2o’, ‘d2o’: Viscosity of the solvent in Pas. (H2O ~ 0.001 Pa*s =1 cPoise) If ‘h2o’ or ‘d2o’ the corresponding viscosity at given temperature is used.
tempfloat: temperature in K.

Returns:

dataArray, dataList: Concentration profile Columns [position in [mm]; conc ; conc_meniscus_part; conc_bottom_part]

Notes

From [1]:”The deviations from the expected results are smaller than 1% for simulated curves and are valid for a great range of molecular masses from 0.4 to at least 7000 kDa. The presented approximate solution, an essential part of LAMM allows the estimation of s and D with an accuracy comparable to that achieved using numerical solutions, e.g the program SEDFIT of Schuck et al.”

Default values are for Heraeus Fresco 21 at 21000g.

References

[1] (1,2)

A new approximate whole boundary solution of the Lamm equation for the analysis of sedimentation velocity experiments J. Behlke, O. Ristau Biophysical Chemistry 95 (2002) 59–68

Examples

Cleaning from aggregates by sedimantation. Sedimentation of protein (R=2 nm) with aggregates of 100nm size.

import numpy as np
import jscatter as js
t1=np.r_[60:1.15e3:11j]  # time in seconds

# open plot()
p=js.grace(1.5,1.5)
p.multi(2,1)

# calculate sedimentation profile for two different particles
# data correspond to Fresco 21 with dual rotor
# default is solvent='h2o',temp=293
g=21000. # g # RZB number
omega=g*246/21000
D2nm=js.formel.sedimentationProfile(t=t1,Rh=2,densitydif=0.37, number=1000)
D50nm=js.formel.sedimentationProfile(t=t1,Rh=50,densitydif=0.37, number=1000)

# plot it
p[0].plot(D2nm,li=[1,2,-1],sy=0,legend='t=$time s' )
p[1].plot(D50nm,li=[1,2,-1],sy=0,legend='t=$time s' )

# pretty up
p[0].yaxis(min=0,max=0.05,label='concentration')
p[1].yaxis(min=0,max=0.05,label='concentration')
p[1].xaxis(label='position mm')
p[0].xaxis(label='')
p[0].text(x=70,y=0.04,string=r'R=2 nm \nno sedimantation')
p[1].text(x=70,y=0.04,string=r'R=50 nm \nfast sedimentation')
p[0].legend(x=42,y=0.05,charsize=0.5)
p[1].legend(x=42,y=0.05,charsize=0.5)
p[0].title('Concentration profile in first {0:} s'.format(np.max(t1)))
p[0].subtitle('2nm and 50 nm particles at 21000g ')
#p.save(js.examples.imagepath+'/sedimentation.jpg')

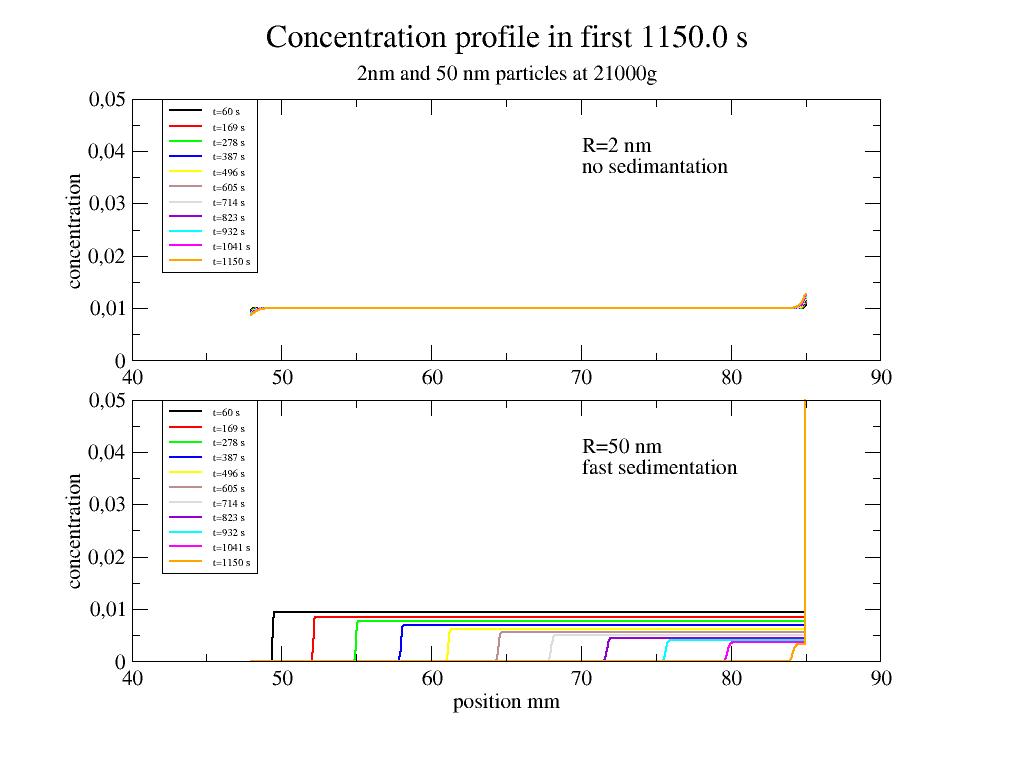
Sedimentation (up concentration) of unilamellar liposomes of DOPC. The density of DOPC is about 1.01 g/ccm in water with 1 g/ccm. Lipid volume fraction is 33% for 50nm radius (10% for 200 nm) for a bilayer thickness of 6.5 nm.

import numpy as np
import jscatter as js

t1=np.r_[100:6e3:11j]  # time in seconds

# open plot()
p=js.grace(1.5,1.5)
p.multi(2,1)

# calculate sedimentation profile for two different particles
# data correspond to Fresco 21 with dual rotor
# default is solvent='h2o',temp=293
g=21000. # g # RZB number
omega=g*246/21000
D100nm=js.formel.sedimentationProfile(t=t1,Rh=50,c0=0.05,omega=omega,rm=48,rb=85,densitydif=0.003)
D400nm=js.formel.sedimentationProfile(t=t1,Rh=200,c0=0.05,omega=omega,rm=48,rb=85,densitydif=0.001)

# plot it
p[0].plot(D100nm,li=[1,2,-1],sy=0,legend='t=$time s' )
p[1].plot(D400nm,li=[1,2,-1],sy=0,legend='t=$time s' )

# pretty up
p[0].yaxis(min=0,max=0.2,label='concentration')
p[1].yaxis(min=0,max=0.2,label='concentration')
p[1].xaxis(label='position mm')
p[0].xaxis(label='')
p[0].text(x=70,y=0.15,string='D=100 nm')
p[1].text(x=70,y=0.15,string='D=400 nm')
p[0].legend(x=42,y=0.2,charsize=0.5)
p[1].legend(x=42,y=0.2,charsize=0.5)
p[0].title('Concentration profile in first {0:} s'.format(np.max(t1)))
p[0].subtitle('at 21000g ')

jscatter.formel.physics.sedimentationProfileFaxen(t=1000.0, rm=48, rb=85, number=100, rlist=None, c0=0.01, s=None, Dt=1.99e-11, w=246, Rh=10, visc='h2o', temp=293, densitydif=None)[source]¶

Faxen solution to the Lamm equation of sedimenting particles in centrifuge; no bottom part.

Bottom equillibrium distribution is not in Faxen solution included. Results in particle distribution along axis for time t.

Parameters:

tfloat: Time after start in seconds. If list, results at these times is given as dataList.
rmfloat: Axial position of meniscus in mm.
rbfloat: Axial position of bottom in mm.
rlistarray, optional: Explicit list of radial values to use between rm=max(rlist) and rb=min(rlist)
numberinteger: Number of points between rm and rb to calculate.
c0float: Initial concentration in cell; just a scaling factor.
sfloat: Sedimentation coefficient in Svedberg; 77 S is r=10 nm particle in H2O.
Dtfloat: Translational diffusion coefficient in m**2/s; 1.99e-11 is r=10 nm particle.
wfloat: Radial velocity rounds per second; 246 rps=2545 rad/s is 20800g in centrifuge fresco 21.
Rhfloat: Hydrodynamic radius in nm ; if given Dt and s are calculated from Rh.
viscfloat, ‘h2o’,’d2o’: Viscosity in units Pas. If ‘h2o’ or ‘d2o’ the corresponding viscosity at given temperature is used.
densitydiffloat: Density difference between solvent and particle in g/ml. Protein in ‘h2o’=> is used =>1.37-1.= 0.37 g/cm**3
tempfloat: temperature in K.

Returns:

dataArray, dataList

Concentration distributiondataArray, dataList: .pelletfraction is the content in pellet as fraction already diffused out .rmeniscus

Notes

Default values are for Heraeus Fresco 21 at 21000g.

References

[1]

Über eine Differentialgleichung aus der physikalischen Chemie. Faxén, H. Ark. Mat. Astr. Fys. 21B:1-6 (1929)

jscatter.formel.physics.viscosity(mat='h2o', T=293.15)[source]¶

Viscosity of pure solvents. For buffer solvents use bufferviscosity.

Parameters:

matstring ‘h2o’,’d2o’,’toluol’,’methylcyclohexan’, default h2o: Solvent
Tfloat: Temperature T in Kelvin default 293K

Returns:

float

viscosity in Pa*s: water H2O ~ 0.001 Pa*s =1 cPoise # Poise=0.1 Pa*s

References

[1]

The Viscosity of Toluene in the Temperature Range 210 to 370 K M. J. Assael, N.K. Dalaouti, J.H., Dymond International Journal of Thermophysics, Vol. 21,291 No. 2, 2000 # accuracy +- 0.4 % laut paper Max error von Experiment data

[2]

Thermal Offset Viscosities of Liquid H2O, D2O, and T2O C. H. Cho, J. Urquidi, S. Singh, and G. Wilse Robinson J. Phys. Chem. B 1999, 103, 1991-1994

jscatter.formel.physics.watercompressibility(d2ofract=1, T=278, units='psnmg')[source]¶

Isothermal compressibility of H2O and D2O mixtures.

Compressibility \(\kappa\) in units ps²nm/g or in 1/bar. Linear mixture according to d2ofract.

Parameters:

d2ofractfloat, default 1: Fraction D2O
Tfloat, default 278K: Temperature in K
unitsstring ‘psnmg’: ps^2*nm/(g/mol) or 1/bar

Returns:

float

Notes

For the structure factor e.g. of water one finds in agreement to literature

\[S(0) = kT n \kappa = 0.064\]

with thermal energy kT and number density n,

\(n = 55.5mol/l = 33.42 /nm³\),
\(kT=300K*1.380649e^{-23} J/K = 414e^{-23} kgm²/s² = 414e^{-26} g nm²/ps²\)
\(\kappa(300K)=4.625e20 g/nm/ps²\)

References

[1]

Isothermal compressibility of Deuterium Oxide at various Temperatures Millero FJ and Lepple FK Journal of chemical physics 54,946-949 (1971) http://dx.doi.org/10.1063/1.1675024

[2]

Precise representation of volume properties of water at one atmosphere G. S. Kell J. Chem. Eng. Data, 1967, 12 (1), pp 66–69 http://dx.doi.org/10.1021/je60032a018

Examples

import jscatter as js
n = js.formel.waterdensity('h2o1',T=300) * 1000/18 *6.023e23/1e24
ka = js.formel.watercompressibility(T=300)
kT = 300*1.380649e-26
S0 = kT*n*ka  # => 0.06388

jscatter.formel.physics.waterdensity(composition, T=293.15, units='mol', showvalidity=False)[source]¶

Density of water with inorganic substances (salts).

Solvent with composition of H2O and D2O and additional inorganic components at temperature T. Ternary solutions allowed. Units are mol

Parameters:

compositionlist of compositional strings

Compositional string of chemical formula as ‘float’+’chemical char’ + integer - First float is content in mol (is later normalised to sum of contents) - chemical letter + number of atoms in formula (single atoms append 1 ,fractional numbers allowed)

'h2o1' or 'd2o1' light and heavy water with 'd1' for deuterium
'c3h8o3' or 'c3h1d7o3' partial deuterated glycerol
['55.55h2o1','2.5Na1Cl1'] for 2.5 mol NaCl added to  1l h2o (55.55 mol)
['20H2O1','35.55D2O1','0.1Na1Cl1'] h2o/d2o mixture with 100mMol NaCl

unitsdefault=’mol’

Anything except ‘mol’ unit is mass fraction ‘mol’ units is mol and mass fraction is calculated as mass=[mol]*mass_of_molecule e.g. 1l Water with 123mM NaCl [‘55.5H2O1’,’0.123Na1Cl1’]

Tfloat, default=293.15

temperature in K

showvaliditybool, default False

Show additionally validity range for temperature and concentration according to [4]. - Temperature range in °C - concentration in wt % or up to a saturated solution (satd) - error in 1/100 % see [4].

Returns:

float: Density in g/ml

Notes

D2O maximum density 1.10596 at T=273.15+11.23 K [1] .
For mixtures of H2O/D2O molar volumes add with an accuracy of about 2e-4 cm**3/mol compared to ~18.015 cm**3/mol molar volume [3].
Additional densities of binary aqueous solutions [4].

Water number density

# 55.5079 mol with 18.015 g/mol
js.formel.waterdensity('1H2O1', T=273+4)*1000/18.015

References

[1]

The dilatation of heavy water K. Stokland, E. Ronaess and L. Tronstad Trans. Faraday Soc., 1939,35, 312-318 DOI: 10.1039/TF9393500312

[2]

Effects of Isotopic Composition, Temperature, Pressure, and Dissolved Gases on the Density of Liquid Water George S. Kell JPCRD 6(4) pp. 1109-1131 (1977)

[3]

Excess volumes for H2O + D2O liquid mixtures Bottomley G Scott R Australian Journal of Chemistry 1976 vol: 29 (2) pp: 427

[4] (1,2,3)

Densities of binary aqueous solutions of 306 inorganic substances P. Novotny, O. Sohnel J. Chem. Eng. Data, 1988, 33 (1), pp 49–55 DOI: 10.1021/je00051a018

availible components:

h2o1 d2o1
TRIS c4h11n1o3
TABS c8h19n1o6s1

     ag1cl104     ag1n1o3      al1cl3012    al1n3o9      al2s3o12     ba1br2      
 ba1cl2       ba1cl2o6     ba1i2        ba1n2o6      c4h11n1o3    c8h19n1o6s1 
 ca1br2       ca1cl2       ca1i2        ca1n2o6      cd1br2       cd1c12      
 cd1i2        cd1n2o6      cd1so4       co1n2o6      co1s1o4      cs1br1      
 cs1cl1       cs1f1        cs1i1        cs1n1o3      cs2s1o4      cu1cl2      
 cu1n2o6      cu1s1o4      dy1cl3       er1cl3       fe1cl3       fe1s1o4     
 gd1cl3       h1br1        h1cl1        h1cl104      h1i1         h1n1o3      
 h2s1o4       h3b103       h3p1o4       hg1c2n2      hg1cl2       k1ag1c2n2   
 k1al1s2o8    k1br1        k1br1o3      k1cl1        k1cl103      k1cl104     
 k1f1         k1h1c1o3     k1h1s1o4     k1h2p1o4     k1i1         k1i103      
 k1mn1o4      k1n1o2       k1n1o3       k1n3         k1o1h1       k1s1c1n1    
 k1tart1      k2c1o3       k2cr104      k2cr207      k2s1o4       k3co1c6n6   
 k3fe1c6n6    k4fe1c6n6    k4mo1c8n8    la1cl3       li1br1       li1cl1      
 li1cl104     li1i1        li1n1o3      li1o1h1      li2s1o4      mg1br2      
 mg1br206     mg1cl2       mg1cl2o8     mg1i2        mg1n2o6      mg1s1o4     
 mn1cl1       mn1s1o4      n1h3         n1h40x1      n1h4ac1      n1h4al1s2o8 
 n1h4cl1      n1h4cl104    n1h4fe1s2o8  n1h4h1s1o4   n1h4h2p1o4   n1h4i1      
 n1h4n1o3     n2h8ni1s2o8  n2h8s1o4     n2s203       na1ac1       na1br1      
 na1br1o3     na1cl1       na1cl103     na1cl104     na1f1        na1form1    
 na1h1s1o4    na1h2p1o4    na1i1        na1i103      na1k1tart1   na1mn104    
 na1n1o2      na1n1o3      na1n3        na1o1h1      na1ox1       na1s1c1n1   
 na1tart1     na2b407      na2c1o3      na2cr1o4     na2cr207     na2h1p1o4   
 na2mo104     na2s1        na2s103      na2s1o4      na2w104      na3p1o4     
 na4p207      na5p307      nd1cl3       ni1cl2       ni1n2o6      ni1s1o4     
 pb1n2o6      pr1cl3       rb1br1       rb1cl1       rb1f1        rb1i1       
 rb1n1o3      rb2so4       sm1cl3       sr1ac2       sr1br2       sr1br206    
 sr1cl2       sr1i2        sr1n2o6      ti1n1o3      ti2s1o4      u1o2n2o6    
 u1o2s104     yb1cl3       zn1br2       zn1cl2       zn1i2        zn1n2o6     
 zn1s1o1     

Physical equations and useful formulas as quadrature of vector functions, parallel execution, viscosity, compressibility of water, scatteringLengthDensityCalc or sedimentationProfile. Use scipy.constants for physical constants.

Each topic is not enough for a single module, so this is a collection.
All scipy functions can be used. See http://docs.scipy.org/doc/scipy/reference/special.html.
Statistical functions http://docs.scipy.org/doc/scipy/reference/stats.html.

Mass and scattering length of all elements in Elements are taken from :

Mass: http://www.chem.qmul.ac.uk/iupac/AtWt/
Neutron scattering length: http://www.ncnr.nist.gov/resources/n-lengths/list.html

Units converted to amu for mass and nm for scattering length.

jscatter.formel.functions.Ea(z, a, b=1)[source]¶

Mittag-Leffler function for real z and real a,b with 0<a, b<0.

Evaluation of the Mittag-Leffler (ML) function with 1 or 2 parameters by means of the OPC algorithm [1]. The routine evaluates an approximation Et of the ML function E such that \(|E-Et|/(1+|E|) \approx 10^{-15}\)

Parameters:

zreal array: Values
afloat, real positive: Parameter alpha
bfloat, real positive, default=1: Parameter beta

Returns:

array

Notes

Mittag Leffler function defined as

\[E(x,a,b)=\sum_{k=0}^{\inf} \frac{z^k}{\Gamma(b+ak)}\]
The code uses code from K.Hinsen at https://github.com/khinsen/mittag-leffler which is a Python port of Matlab implementation of the generalized Mittag-Leffler function as described in [1].
The function cannot be simply calculated by using the above summation. This fails for a,b<0.7 because of various numerical problems. The above implementation of K.Hinsen is the best availible approximation in Python.

References

[1]

R. Garrappa, Numerical evaluation of two and three parameter Mittag-Leffler functions, SIAM Journal of Numerical Analysis, 2015, 53(3), 1350-1369

Examples

import numpy as np
import jscatter as js
from scipy import special
x=np.r_[-10:10:0.1]
# tests
np.all(js.formel.Ea(x,1,1)-np.exp(x)<1e-10)
z = np.linspace(0., 2., 50)
np.allclose(js.formel.Ea(np.sqrt(z), 0.5), np.exp(z)*special.erfc(-np.sqrt(z)))
z = np.linspace(-2., 2., 50)
np.allclose(js.formel.Ea(z**2, 2.), np.cosh(z))

jscatter.formel.functions.boseDistribution(w, temp)[source]¶

Bose distribution for integer spin particles in non-condensed state (hw>0).

\[ \begin{align}\begin{aligned}n(w) &= \frac{1}{e^{hw/kT}-1} &\ hw>0\\ &= 0 &\: hw=0 \: This is not real just for convenience!\end{aligned}\end{align} \]

Parameters:

warray: Frequencies in units 1/ns
tempfloat: Temperature in K

Returns:

dataArray

jscatter.formel.functions.box(x, edges=None, edgevalue=0, rtol=1e-05, atol=1e-08)[source]¶

Box function.

For equal edges and edge value > 0 the delta function is given.

Parameters:

xarray
edgeslist of float, float, default=[0]: Edges of the box. If only one number is given the box goes from [-edge:edge]
edgevaluefloat, default=0: Value to use if x==edge for both edges.
rtol,atolfloat: The relative/absolute tolerance parameter for the edge detection. See numpy.isclose.

Returns:

dataArray

Notes

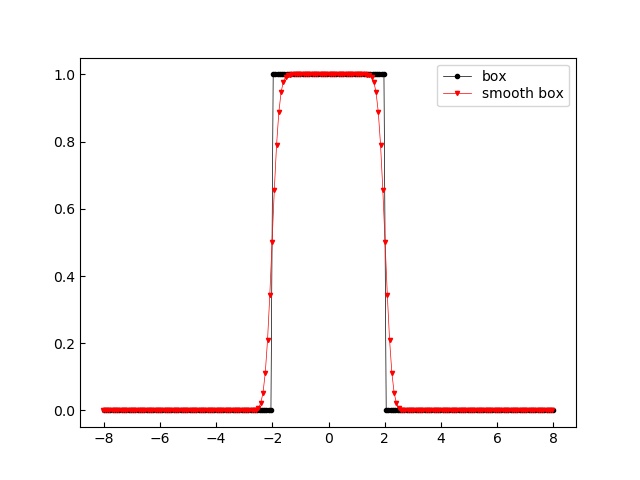
Edges may be smoothed by convolution with a Gaussian.:

import jscatter as js
import numpy as np
edge=2
x=np.r_[-4*edge:4*edge:200j]
f=js.formel.box(x,edges=edge)
res=js.formel.convolve(f,js.formel.gauss(x,0,0.2))
#
p=js.mplot()
p.Plot(f,li=1,le='box')
p.Plot(res,li=2,le='smooth box')
p.Legend()
#p.savefig(js.examples.imagepath+'/box.jpg')

jscatter.formel.functions.eijk = array([[[ 0., 0., 0.], [ 0., 0., 1.], [ 0., -1., 0.]], [[ 0., 0., -1.], [ 0., 0., 0.], [ 1., 0., 0.]], [[ 0., 1., 0.], [-1., 0., 0.], [ 0., 0., 0.]]])¶: Antisymmetric Levi-Civita symbol

jscatter.formel.functions.gauss(x, mean=1, sigma=1)[source]¶

Normalized Gaussian function.

\[g(x)= \frac{1}{sigma\sqrt{2\pi}} e^{-0.5(\frac{x-mean}{sigma})^2}\]

Parameters:

xfloat: Values
meanfloat: Mean value
sigmafloat: 1/e width. Negative values result in negative amplitude.

Returns:

dataArray

jscatter.formel.functions.lognorm(x, mean=1, sigma=1)[source]¶

Lognormal distribution function.

\[f(x>0)= \frac{1}{\sqrt{2\pi}\sigma x }\,e^{ -\frac{(\ln(x)-\mu)^2}{2\sigma^2}}\]

Parameters:

xarray: x values
meanfloat: mean
sigmafloat: sigma

Returns:

dataArray

jscatter.formel.functions.lorentz(x, mean=1, gamma=1)[source]¶

Normalized Lorentz function

\[f(x) = \frac{gamma}{\pi((x-mean)^2+gamma^2)}\]

Parameters:

xarray: X values
gammafloat: Half width half maximum
meanfloat: Mean value

Returns:

dataArray

jscatter.formel.functions.schulzDistribution(r, mean, sigma)[source]¶

Schulz (or Gamma) distribution for polymeric particles/chains.

Distribution describing a polymerisation like radical polymerization:

constant number of chains growth till termination.
concentration of active centers constant.
start of chain growth not necessarily at the same time.
In polymer physics sometimes called Schulz-Zimm distribution. Same as Gamma distribution.

Parameters:

rarray: Distribution variable such as relative molecular mass or degree of polymerization, number of monomers.
meanfloat: Mean \(<r>\)
sigmafloat: Width as standard deviation \(s=\sqrt{<r^2>-<r>^2}\) of the distribution. \(z = (<r>/s)^2 -1 < 600\)

Returns:

dataArrayColumns [x,p]

.z ==> z+1 = k is degree of coupling = number of chain combined to dead chain in termination reaction
z = (<r>/s)² -1

Notes

The Schulz distribution [1]

\[h(r) = \frac{(z+1)^{z+1}r^z}{(mean^{z+1}\Gamma(z+1)}e^{-(z+1)\frac{r}{mean}}\]

alternatively with \(a=<r>^2/s^2\) and \(b=a/<r>\)

\[h(r) = \frac{b^a r^(a-1)}{(\Gamma(a)}e^{-br}\]

Normalized to \(\int h(r)dr=1\).

Nth order average \(<r>^n = \frac{z+n}{z+1} <r>\)

number average \(<r>^1 = <r>\)
weight average \(<r>^2 = \frac{z+2}{z+1} <r>\)
z average \(<r>^3 = \frac{z+3}{z+1} <r>\)

References

[1]

Schulz, G. V. Z. Phys. Chem. 1939, 43, 25

[2]

Theory of dynamic light scattering from polydisperse systems S. R. Aragón and R. Pecora The Journal of Chemical Physics, 64, 2395 (1976)

Examples

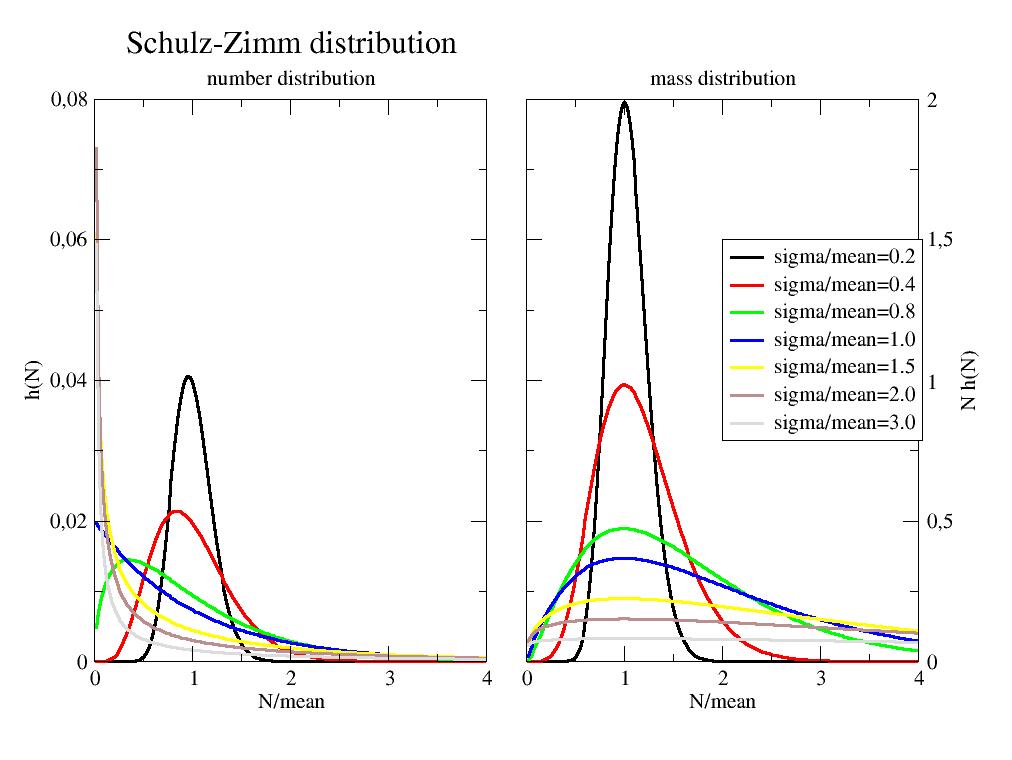
import jscatter as js
import numpy as np
N=np.r_[1:200]
p=js.grace(1.4,1)
p.multi(1,2)
m=50
for i,s in enumerate([10,20,40,50,75,100,150],1):
    SZ = js.formel.schulzDistribution(N,mean=m,sigma=s)
    p[0].plot(SZ.X/m,SZ.Y,sy=0,li=[1,3,i],le=f'sigma/mean={s/m:.1f}')
    p[1].plot(SZ.X/m,SZ.Y*SZ.X,sy=0,li=[1,3,i],le=f'sigma/mean={s/m:.1f}')
p[0].xaxis(label='N/mean')
p[0].yaxis(label='h(N)')
p[0].subtitle('number distribution')
p[1].xaxis(label='N/mean')
p[1].yaxis(label='N h(N)')
p[1].subtitle('mass distribution')
p[1].legend(x=2,y=1.5)
p[0].title('Schulz distribution')
#p.save(js.examples.imagepath+'/schulzZimm.jpg')

jscatter.formel.functions.voigt(x, center=0, fwhm=1, lg=1, asym=0, amplitude=1)[source]¶

Voigt function for peak analysis (normalized).

The Voigt function is a convolution of gaussian and lorenzian shape peaks for peak analysis. The Lorenzian shows a stronger contribution outside FWHM with a sharper peak. Asymmetry of the shape can be added by a sigmoidal change of the FWHM [2].

Parameters:

xarray

Axis values.

centerfloat

Center of the distribution.

fwhmfloat

Full width half maximum of the Voigt function.

lgfloat, default = 1

Lorenzian/gaussian fraction of both FWHM, describes the contributions of gaussian and lorenzian shape.

lorenzian/gaussian >> 1 lorenzian,
lorenzian/gaussian ~ 1 central part gaussian, outside lorenzian wings
lorenzian/gaussian << 1. gaussian

asymfloat, default=0

Asymmetry factor in sigmoidal as \(fwhm_{asym} = 2*fwhm/(1+np.exp(asym*(x-center)))\) . For a=0 the Voigt is symmetric.

amplitudefloat, default = 1

amplitude

Returns:

dataArray: .center .sigma .gamma .fwhm .asymmetry .lorenzianOverGaussian (lg)

Notes

The Voigt function is a convolution of Gaussian and Lorentz functions

\[G(x;\sigma) = e^{-x^2/(2\sigma^2)}/(\sigma \sqrt{2\pi})\ and \ L(x;\gamma) = \gamma/(\pi(x^2+\gamma^2))\]

resulting in

\[V(x;\sigma,\gamma)=\frac{\operatorname{Re}[w(z)]}{\sigma\sqrt{2 \pi}}\]

with \(z=(x+i\gamma)/(\sigma\sqrt{2})\) and \(Re[w(z)]\) is the real part of the Faddeeva function.

\(\gamma\) is the Lorentz fwhm width and \(fwhm=(2\sqrt{2\ln 2})\sigma\) the Gaussian fwhm width.

The FWHM in Lorentz and Gaussian dependent on the fwhm of the Voigt function is \(fwhm_{Gauss,Lorentz} \approx fwhm / (0.5346 lg + (0.2166 lg^2 + 1)^{1/2})\) (accuracy 0.02%).

References

[1]

https://en.wikipedia.org/wiki/Voigt_profile

[2]

A simple asymmetric lineshape for fitting infrared absorption spectra Aaron L. Stancik, Eric B. Brauns Vibrational Spectroscopy 47 (2008) 66–69

[3]

Empirical fits to the Voigt line width: A brief review Olivero, J. J.; R. L. Longbothum Journal of Quantitative Spectroscopy and Radiative Transfer. 17, 233–236. doi:10.1016/0022-4073(77)90161-3

Physical equations and useful formulas as quadrature of vector functions, parallel execution, viscosity, compressibility of water, scatteringLengthDensityCalc or sedimentationProfile. Use scipy.constants for physical constants.

Each topic is not enough for a single module, so this is a collection.
All scipy functions can be used. See http://docs.scipy.org/doc/scipy/reference/special.html.
Statistical functions http://docs.scipy.org/doc/scipy/reference/stats.html.

Mass and scattering length of all elements in Elements are taken from :

Mass: http://www.chem.qmul.ac.uk/iupac/AtWt/
Neutron scattering length: http://www.ncnr.nist.gov/resources/n-lengths/list.html

Units converted to amu for mass and nm for scattering length.

jscatter.formel.quadrature.convolve(A, B, mode='same', normA=False, normB=False)[source]¶

Convolve A and B with proper tracking of the output X axis.

Approximate the convolution integral as the discrete, linear convolution of two one-dimensional sequences. Missing values are linear interpolated to have matching steps. Values outside of X ranges are set to zero.

Parameters:

A,BdataArray, ndarray

To be convolved arrays (length N and M).

dataArray convolves Y with Y values
ndarray A[0,:] is X and A[1,:] is Y

normA,normBbool, default False

Determines if A or B should be normalised that \(\int_{x_{min}}^{x_{max}} A(x) dx = 1\).

mode‘full’,’same’,’valid’, default ‘same’

See example for the difference in range.

‘full’ Returns the convolution at each point of overlap,
with an output shape of (N+M-1,). At the end-points of the convolution, the signals do not overlap completely, and boundary effects may be seen.
‘same’ Returns output of length max(M, N).
Boundary effects are still visible.
‘valid’ Returns output of length M-N+1.

Returns:

dataArray: with attributes from A

Notes

\(A\circledast B (t)= \int_{-\infty}^{\infty} A(x) B(t-x) dx = \int_{x_{min}}^{x_{max}} A(x) B(t-x) dx\)
If A,B are only 1d array use np.convolve.
If attributes of B are needed later use .setattr(B,’B-’) to prepend ‘B-’ for B attributes.

References

[1]

Wikipedia, “Convolution”, http://en.wikipedia.org/wiki/Convolution.

Examples

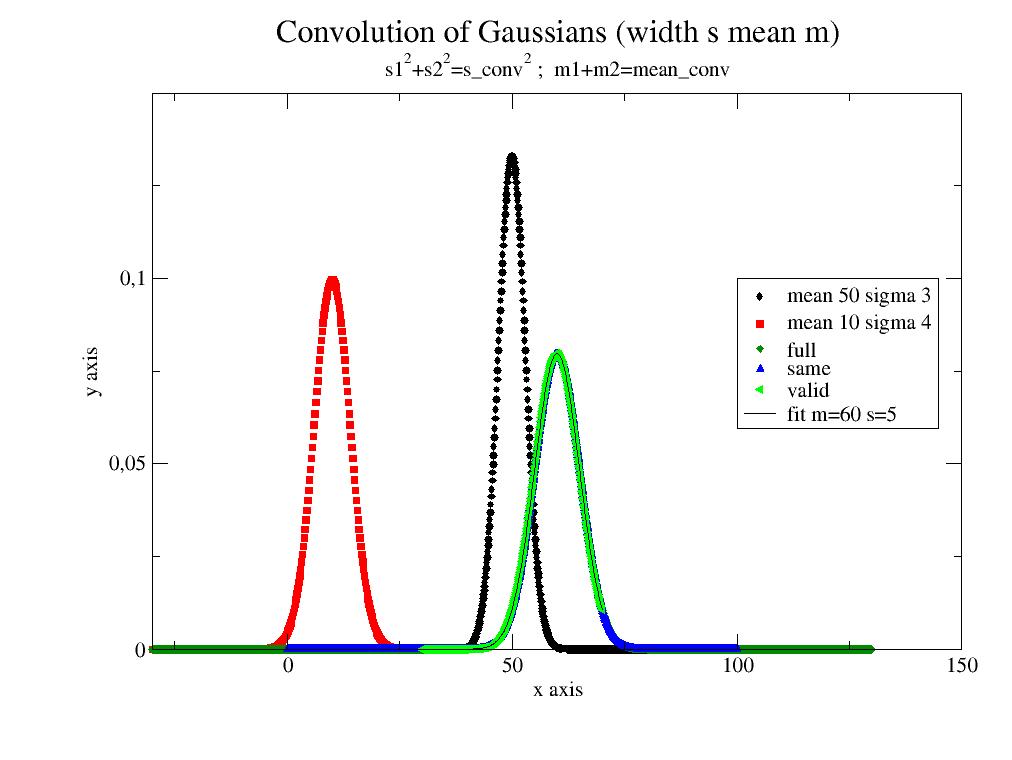
Demonstrate the difference between modes

import jscatter as js;import numpy as np
s1=3;s2=4;m1=50;m2=10
G1=js.formel.gauss(np.r_[0:100.1:0.1],mean=m1,sigma=s1)
G2=js.formel.gauss(np.r_[-30:30.1:0.2],mean=m2,sigma=s2)
p=js.grace()
p.title('Convolution of Gaussians (width s mean m)')
p.subtitle(r's1\S2\N+s2\S2\N=s_conv\S2\N ;  m1+m2=mean_conv')
p.plot(G1,le='mean 50 sigma 3')
p.plot(G2,le='mean 10 sigma 4')
ggf=js.formel.convolve(G1,G2,'full')
p.plot(ggf,le='full')
gg=js.formel.convolve(G1,G2,'same')
p.plot(gg,le='same')
gg=js.formel.convolve(G1,G2,'valid')
p.plot(gg,le='valid')
gg.fit(js.formel.gauss,{'mean':40,'sigma':1},{},{'x':'X'})
p.plot(gg.modelValues(),li=1,sy=0,le='fit m=$mean s=$sigma')
p.legend(x=100,y=0.1)
p.xaxis(max=150,label='x axis')
p.yaxis(min=0,max=0.15,label='y axis')
p.save(js.examples.imagepath+'/convolve.jpg')

jscatter.formel.quadrature.multiParDistributedAverage(funktion, sigs, parnames, types='normal', N=30, ncpu=1, **kwargs)[source]¶

Vectorized average assuming multiple parameters are distributed in intervals. Shortcut mPDA.

Function average over multiple distributed parameters with weights determined from probability distribution. The probabilities for the parameters are multiplied as weights and a weighted sum is calculated by Monte-Carlo integration.

Parameters:

funktionfunction

Function to integrate with distribution weight.

sigslist of float

List of widths for parameters. Sigs are the standard deviation from mean (or root of variance), see Notes.

parnamesstring

List of names of the parameters which show a distribution.

typeslist of ‘normal’, ‘lognorm’, ‘gamma’, ‘lorentz’, ‘uniform’, ‘poisson’, ‘schulz’, ‘duniform’, default ‘normal’

List of types of the distributions. If types list is shorter than parnames the last is repeated.

kwargsparameters

Any additonal kword parameter to pass to function. The value of parnames that are distributed will be the mean value of the distribution.

Nfloat , default=30

Number of points over distribution ranges. Distributions are integrated in probability intervals \([e^{-4} \ldots 1-e^{-4}]\).

ncpuint, default=1, optional

Number of cpus in the pool for parallel excecution. Set this to 1 if the integrated function uses multiprocessing to avoid errors.

0 -> all cpus are used

int>0 min (ncpu, mp.cpu_count)

int<0 ncpu not to use

Returns:

dataArray

as returned from function with

.parname_mean = mean of parname
.parname_std = standard deviation of parname

Notes

Calculation of an average over D multiple distributed parameters by conventional integration requires \(N^D\) function evaluations which is quite time consuming. Monte-Carlo integration at N points with random combinations of parameters requires only N evaluations.

The given function of fixed parameters \(q_j\) and polydisperse parameters \(p_i\) with width \(s_i\) related to the indicated distribution (types) is integrated as

\[f_{mean}(q_j,p_i,s_i) = \frac{\sum_h{f(q_j,x^h_i)\prod_i{w_i(x^h_i)}}}{\sum_h \prod_i w_i(x^h_i)}\]

Each parameter \(p_i\) is distributed along values \(x^h_i\) with probability \(w_i(x^h_i)\) describing the probability distribution with mean \(p_i\) and sigma \(s_i\). Intervals for a parameter \(p_i\) are choosen to represent the distribution in the interval \([w_i(x^0_i) = e^{-4} \ldots \sum_h w_i(x^h_i) = 1-e^{-4}]\)

The distributed values \(x^h_i\) are determined as pseudorandom numbers of N points with dimension len(i) for Monte-Carlo integration.

For a single polydisperse parameter use parDistributedAverage.
During fitting it has to be accounted for the information content of the experimental data. As in the example below it might be better to use a single width for all parameters to reduce the number of redundant parameters.

The used distributions are from scipy.stats. Choose the distribution according to the problem and check needed number of points N.

mean is the value in kwargs[parname]. mean is the expectation value of the distributed variable and sig² are the variance as the expectation of the squared deviation from the mean. Distributions may be parametrized differently :

norm :

mean , std

stats.norm(loc=mean,scale=sig)
lognorm :

mean and sig evaluate to mean and std

mu=math.log(mean**2/(sig+mean**2)**0.5)

nu=(math.log(sig/mean**2+1))**0.5

stats.lognorm(s=nu,scale=math.exp(mu))
gamma :

mean and sig evaluate to mean and std

stats.gamma(a=mean**2/sig**2,scale=sig**2/mean)

Same as SchulzZimm
lorentz = cauchy:

mean and std are not defined. Use FWHM instead to describe width.

sig=FWHM

stats.cauchy(loc=mean,scale=sig))
uniform :

Continuous distribution.

sig is width

stats.uniform(loc=mean-sig/2.,scale=sig))
poisson:
stats.poisson(mu=mean,loc=sig)
schulz

same as gamma
duniform:

Uniform distribution integer values.

sig>1

stats.randint(low=mean-sig, high=mean+sig)

For more distribution look into this source code and use it appropriate with scipy.stats.

Examples

The example of a cuboid with independent polydispersity on all edges. To use the function in fitting please encapsulate it in a model function hiding the list parameters.

import jscatter as js
type=['norm','schulz']
p=js.grace()
q=js.loglist(0.1,5,500)
sp=js.ff.cuboid(q=q,a=4,b=4.1,c=4.3)
p.plot(sp,sy=[1,0.2],legend='single cube')
p.yaxis(scale='l',label='I(Q)')
p.xaxis(scale='n',label='Q / nm')

def cub(q,a,b,c):
   a = js.ff.cuboid(q=q,a=a,b=b,c=c)
   return a

p.title('Cuboid with independent polydispersity on all 3 edges')
p.subtitle('Using Monte Carlo integration; 30 points are enough here!')
sp1=js.formel.mPDA(cub,sigs=[0.2,0.3,0.1],parnames=['a','b','c'],types=type,q=q,a=4,b=4.1,c=4.2,N=10)
p.plot(sp1,li=[1,2,2],sy=0,legend='normal 10 points')
sp2=js.formel.mPDA(cub,sigs=[0.2,0.3,0.1],parnames=['a','b','c'],types=type,q=q,a=4,b=4.1,c=4.2,N=30)
p.plot(sp2,li=[1,2,3],sy=0,legend='normal 30 points')
sp3=js.formel.mPDA(cub,sigs=[0.2,0.3,0.1],parnames=['a','b','c'],types=type,q=q,a=4,b=4.1,c=4.2,N=90)
p.plot(sp3,li=[3,2,4],sy=0,legend='normal 100 points')
p.legend(x=2,y=1000)
# p.save(js.examples.imagepath+'/multiParDistributedAverage.jpg')

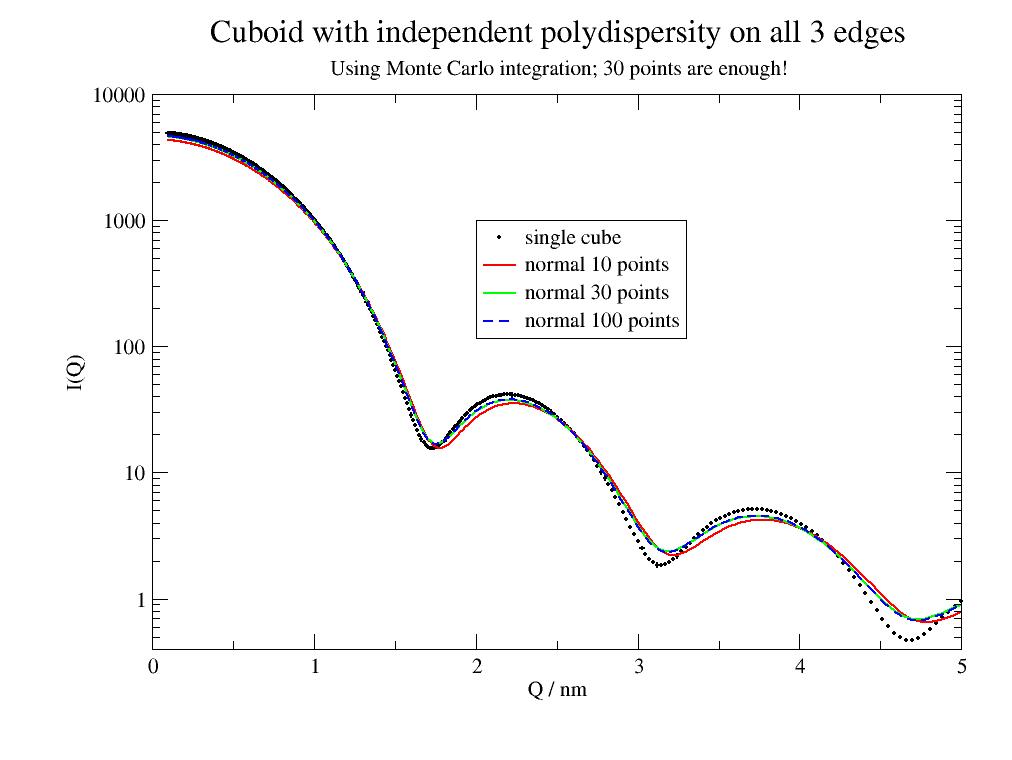
During fitting encapsulation might be done like this

def polyCube(a,b,c,sig,N):
   res = js.formel.mPDA(js.ff.cuboid,sigs=[sig,sig,sig],parnames=['a','b','c'],types='normal',q=q,a=a,b=b,c=c,N=N)
   return res

jscatter.formel.quadrature.parAdaptiveCubature(func, lowlimit, uplimit, parnames, fdim=None, adaptive='p', abserr=1e-08, relerr=0.001, *args, **kwargs)[source]¶

Vectorized adaptive multidimensional integration (cubature). Shortcut pAC.

We use the cubature module written by SG Johnson [2] for h-adaptive (recursively partitioning the integration domain into smaller subdomains) and p-adaptive (Clenshaw-Curtis quadrature, repeatedly doubling the degree of the quadrature rules). This function is a wrapper around the package cubature which can be used also directly.

Parameters:

funcfunction

The function to integrate. The return array needs to be an 2-dim array with the last dimension as vectorized return (=len(fdim)) and first along the points of the parnames parameters to integrate. Use numpy functions for array functions to speedup computations. See example.

parnameslist of string

Parameter names of variables to integrate. Should be scalar.

lowlimitlist of float

Lower limits of the integration variables with same length as parnames.

uplimit: list of float

Upper limits of the integration variables with same length as parnames.

fdimint, None, optional

Second dimension size of the func return array. If None, the function is evaluated with the uplimit values to determine the size. For complex valued function it is twice the complex array length.

adaptive‘h’, ‘p’, default=’p’

Type of adaption algorithm.

‘h’ Multidimensional h-adaptive integration by subdividing the integration interval into smaller intervals
where the same rule is applied. The value and error in each interval is calculated from 7-point rule and difference to 5-point rule. For higher dimensions only the worst dimension is subdivided [3]. This algorithm is best suited for a moderate number of dimensions (say, < 7), and is superseded for high-dimensional integrals by other methods (e.g. Monte Carlo variants or sparse grids).
‘p’ Multidimensional p-adaptive integration by increasing the degree of the quadrature rule according to
Clenshaw-Curtis quadrature (in each iteration the number of points is doubled and the previous values are reused). Clenshaw-Curtis has similar error compared to Gaussian quadrature even if the used error estimate is worse. This algorithm is often superior to h-adaptive integration for smooth integrands in a few (≤ 3) dimensions,

abserr, relerrfloat default = 1e-8, 1e-3

Absolute and relative error to stop. The integration will terminate when either the relative OR the absolute error tolerances are met. abserr=0, which means that it is ignored. The real error is much smaller than this stop criterion.

maxEvalint, default 0, optional

Maximum number of function evaluations. 0 is infinite.

normint, default=None, optional

Norm to evaluate the error.

None: 0,1 automatically choosen for real or complex functions.
0: individual for each integrand (real valued functions)
1: paired error (L2 distance) for complex values as distance in complex plane.
Other values as mentioned in cubature documentation.

args,kwargsoptional

Additional arguments and keyword arguments passed to func.

Returns:

arrays values , error

Notes

The here used module jscatter.libs.cubature is an adaption of the Python interface of S.G.P. Castro [1] (vers. 0.14.5) to access the C-module of S.G. Johnson [2] (vers. 1.0.3). Only the vectorized form is realized here. The advantage here are fewer dependencies during install. Check the original packages for detailed documentation or look in jscatter.libs.cubature how to use it for your own things.
Internal: For complex valued functions the complex has to be split in real and imaginary to pass to the integration and later the result has to be converted to complex again. This is done automatically dependent on the return value of the function. For the example the real valued function is about 9 times faster

References

[1]

https://github.com/saullocastro/cubature

[2] (1,2)

https://github.com/stevengj/cubature

[3]

An adaptive algorithm for numeric integration over an N-dimensional rectangular region A. C. Genz and A. A. Malik, J. Comput. Appl. Math. 6 (4), 295–302 (1980).

[4]

https://en.wikipedia.org/wiki/Clenshaw-Curtis_quadrature

Examples

Integration of the sphere to get the sphere formfactor. In the first example the symmetry is used to return real valued amplitude. In the second the complex amplitude is used. Both can be compared to the analytic formfactor. Errors are much smaller than the abserr/relerr stop criterion. The stop seems to be related to the minimal point at q=2.8 as critical point. h-adaptive is for dim=3 less accurate and slower than p-adaptive.

The integrands contain patterns of scheme q[:,None]*theta (with later .T to transpose, alternative q*theta[:,None]) to result in a 2-dim array with the last dimension as vectorized return. The first dimension goes along the points to evaluate as determined from the algorithm.

import jscatter as js
import numpy as np
R=5
q = np.r_[0.01:3:0.02]

def sphere_real(r, theta, phi, b, q):
    res = b*np.cos(q[:,None]*r*np.cos(theta))*r**2*np.sin(theta)*2
    return res.T

pn = ['r','theta','phi']
fa_r,err = js.formel.pAC(sphere_real, [0,0,0], [R,np.pi/2,np.pi*2], pn, b=1, q=q)
fa_rh,errh = js.formel.pAC(sphere_real, [0,0,0], [R,np.pi/2,np.pi*2], pn, b=1, q=q,adaptive='h')

# As complex function
def sphere_complex(r, theta, phi, b, q):
    fac = b * np.exp(1j * q[:, None] * r * np.cos(theta)) * r ** 2 * np.sin(theta)
    return fac.T

fa_c, err = js.formel.pAC(sphere_complex, [0, 0, 0], [R, np.pi, np.pi * 2], pn, b=1, q=q)

sp = js.ff.sphere(q, R)
p = js.grace()
p.multi(2,1,vgap=0)

# integrals
p[0].plot(q, fa_r ** 2, le='real integrand p-adaptive')
p[0].plot(q, fa_rh ** 2, le='real integrand h-adaptive')
p[0].plot(q, np.real(fa_c * np.conj(fa_c)),sy=[8,0.5,3], le='complex integrand')
p[0].plot(q, sp.Y, li=1, sy=0, le='analytic')

# errors
p[1].plot(q,np.abs(fa_r**2 -sp.Y), le='real integrand')
p[1].plot(q,np.abs(fa_rh**2 -sp.Y), le='real integrand h-adaptive')
p[1].plot(q,np.abs(np.real(fa_c * np.conj(fa_c)) -sp.Y),sy=[8,0.5,3],le='complex p-adaptive')

p[0].yaxis(scale='l',label='F(q)',ticklabel=['power',0])
p[0].xaxis(ticklabel=0)
p[0].legend(x=2,y=1e6)
p[1].legend(x=2.1,y=5e-9,charsize=0.8)
p[1].yaxis(scale='l',label=r'error', ticklabel=['power',0],min=1e-13,max=5e-6)
p[1].xaxis(label=r'q / nm\S-1')
p[1].text(r'error = abs(F(Q) - F(q)\sanalytic\N)',x=0.8,y=1e-9,charsize=1)
p[0].title('Numerical quadrature sphere formfactor ')
p[0].subtitle('stop criterion relerror=1e-3, real errors are smaller')
#p.save(js.examples.imagepath+'/cubature.jpg')

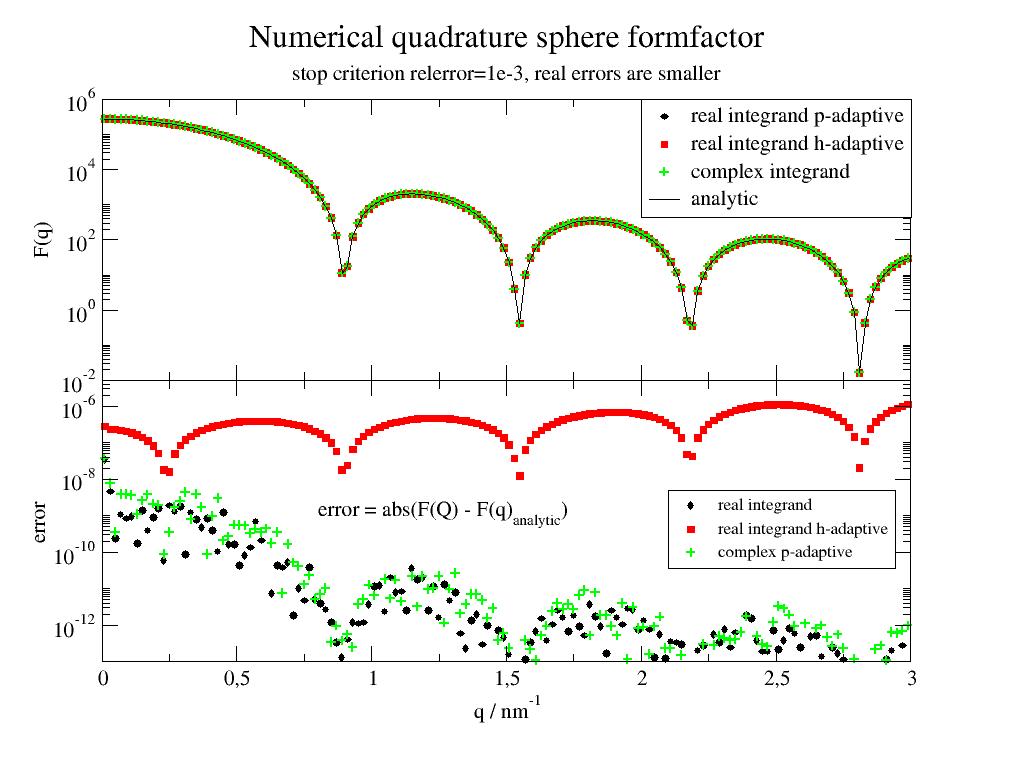
jscatter.formel.quadrature.parDistributedAverage(funktion, sig, parname, type='norm', nGauss=30, **kwargs)[source]¶

Vectorized average assuming a single parameter is distributed with width sig. Shortcut pDA.

Function average over a parameter with weights determined from probability distribution. Gaussian quadrature over given distribution or summation with weights is used. All columns are integrated except .X for dataArray.

Parameters:

funktionfunction

Function to integrate with distribution weight. Function needs to return dataArray. All columns except .X are integrated.

sigfloat

Standard deviation from mean (root of variance) or location describing the width the distribution, see Notes.

parnamestring

Name of the parameter of funktion which shows a distribution.

type‘normal’,’lognorm’,’gamma’,’lorentz’,’uniform’,’poisson’,’schulz’,’duniform’,’truncnorm’ default ‘norm’

Type of the distribution

kwargsparameters

Any additional keyword parameter to pass to function or distribution. The value of parname will be the mean value of the distribution.

nGaussfloat , default=30

Order of quadrature integration as number of intervals in Gauss–Legendre quadrature over distribution. Distribution is integrated in probability interval [0.001..0.999].

ncpuint, optional

Number of cpus in the pool. Set this to 1 if the integrated function uses multiprocessing to avoid errors.

0 -> all cpus are used

int>0 min (ncpu, mp.cpu_count)

int<0 ncpu not to use

Returns:

outdataArray

as returned from function with

.parname_mean : mean of parname
.parname_std : standard deviation of parname (root of variance, input parameter)
.pdf : probability distribution within some range.

Notes

The used distributions are from scipy.stats. Choose the distribution according to the problem.

mean is the value in kwargs[parname]. mean is the expectation value of the distributed variable.
sig² is the variance as the expectation of the squared deviation from the mean.

Distributions may be parametrized differently with additional parameters :

norm :

mean , sig

stats.norm(loc=mean,scale=sig)

here sig scales the position
truncnorm

mean , sig; a,b lower and upper cutoffs

a,b are in scale of sig around mean;

absolute cutoff c,d change to a, b = (c-mean)/sig, (d-mean)/sig

stats.norm(a,b,loc=mean,scale=sig)
lognorm :

mean and sig evaluate to (see https://en.wikipedia.org/wiki/Log-normal_distribution)

a = 1 + (sig / mean) ** 2

s = np.sqrt(np.log(a))

scale = mean / np.sqrt(a)

stats.lognorm(s=s,scale=scale)
gamma :

mean and sig

stats.gamma(a=mean**2/sig**2,scale=sig**2/mean)

Same as SchulzZimm
lorentz = cauchy :

mean and sig are not defined. Use FWHM instead to describe width.

sig=FWHM

stats.cauchy(loc=mean,scale=sig))
uniform :

Continuous distribution.

sig is width

stats.uniform(loc=mean-sig/2.,scale=sig))
schulz

Same as gamma
poisson:
stats.poisson(mu=mean,loc=sig)
duniform:

Uniform distribution integer values.

sig>1

stats.randint(low=mean-sig, high=mean+sig)

For more distribution look into this source code and use it appropriate with scipy.stats.

Examples

import jscatter as js
p=js.grace()
q=js.loglist(0.1,5,500)
sp=js.ff.sphere(q=q,radius=5)
p.plot(sp,sy=[1,0.2],legend='single radius')
p.yaxis(scale='l',label='I(Q)')
p.xaxis(scale='n',label='Q / nm')
sig=0.2
p.title('radius distribution with width %.g' %(sig))

sp2=js.formel.pDA(js.ff.sphere,sig,'radius',type='norm',q=q,radius=5,nGauss=100)
p.plot(sp2,li=[1,2,2],sy=0,legend='normal 100 points Gauss ')

sp4=js.formel.pDA(js.ff.sphere,sig,'radius',type='normal',q=q,radius=5,nGauss=30)
p.plot(sp4,li=[1,2,3],sy=0,legend='normal 30 points Gauss  ')

sp5=js.formel.pDA(js.ff.sphere,sig,'radius',type='normal',q=q,radius=5,nGauss=5)
p.plot(sp5,li=[1,2,5],sy=0,legend='normal 5 points Gauss  ')

sp3=js.formel.pDA(js.ff.sphere,sig,'radius',type='lognorm',q=q,radius=5)
p.plot(sp3,li=[3,2,4],sy=0,legend='lognorm')

sp6=js.formel.pDA(js.ff.sphere,sig,'radius',type='gamma',q=q,radius=5)
p.plot(sp6,li=[2,2,6],sy=0,legend='gamma ')

sp9=js.formel.pDA(js.ff.sphere,sig,'radius',type='schulz',q=q,radius=5)
p.plot(sp9,li=[3,2,2],sy=0,legend='SchulzZimm ')

# an unrealistic example
sp7=js.formel.pDA(js.ff.sphere,1,'radius',type='poisson',q=q,radius=5)
p.plot(sp7,li=[1,2,6],sy=0,legend='poisson ')

sp8=js.formel.pDA(js.ff.sphere,1,'radius',type='duniform',q=q,radius=5)
p.plot(sp8,li=[1,2,6],sy=0,legend='duniform ')
p.legend()

jscatter.formel.quadrature.parQuadratureAdaptiveClenshawCurtis(func, lowlimit, uplimit, parnames, weights0=None, weights1=None, weights2=None, rtol=1e-06, tol=1e-12, maxiter=520, miniter=8, **kwargs)[source]¶

Vectorized adaptive multidimensional Clenshaw-Curtis quadrature for 1-3 dimensions. Shortcut pQACC.

Clenshaw-Curtis is superior to adaptive Gauss as for increased order the already calculated function values are reused. Convergence is similar to adaptive Gauss. In the cuboid example CC is about 3 times faster.

Parameters:

funcfunction

A function or method to integrate. The return array needs to be a 2-dim array with the last dimension as vectorized return and first along the points of the parnames to integrate. Use numpy functions for array functions to speedup computations. See example.

lowlimitlist of float

Lower limits of integration.

uplimitlist of float

Upper limits of integration.

parnameslist of strings

Names of the integration variables which should be scalar.

weights0,weights1,weights2ndarray shape(2,N),default=None

Weights for integration along parname as a e.g. Gaussian distribution with a<weights[0]<b and weights[1] contains weight values.
Missing values are linear interpolated (faster).

If None equal weights=1 are used.

kwargsdict, optional

Extra keyword arguments to pass to function, if any.

tol, rtolfloat, optional

Iteration stops when (average) error between last two iterates is less than tol OR the relative change is less than rtol.

maxiterint, default 520, optional

Maximum order of quadrature. Remember that the array of function values is of size iter**dim .

miniterint, default 8, optional

Minimum order of quadrature.

Returns:

arrays values, error

Notes

Convergence of Clenshaw Curtis is about the same as Gauss-Legendre [1],[Rf60c51bb70ab-2]_.
The iterative procedure reuses the previous calculated function values corresponding to F(n//2). Therefore eCC is faster
Error estimates are based on the difference between F(n) and F(n//2) which is on the order of other more sophisticated estimates [2].
Curse of dimension: The error for d-dim integrals is of order \(O(N^{-r/d})\) if the 1-dim integration method is \(O(N^{-r})\) with N as number of evaluation points in d-dim space. For Clenshaw-Curtis r is about 3 [2].
For higher dimensions used Monte-Carlo Methods (e.g. with pseudo random numbers).

References

[1]

https://en.wikipedia.org/wiki/Clenshaw-Curtis_quadrature

[2] (1,2)

Error estimation in the Clenshaw-Curtis quadrature formula H. O’Hara and Francis J. Smith The Computer Journal, 11, 213–219 (1968), https://doi.org/10.1093/comjnl/11.2.213

[3]

Monte Carlo theory, methods and examples, chapter 7 Other quadrature methods Art B. Owen, 2019 https://statweb.stanford.edu/~owen/mc/

Examples

The cuboid formfactor includes an orientational average over the unit sphere which is done by integration over angles phi and theta which are our scalar integration variables. The array of q values are our vector input as we want to integrate for all q.

The integrand cuboid contains patterns of scheme q*theta[:,None] to result in a 2-dim array with the last dimension as vectorized return. The first dimension goes along the points to evaluate as determined from the algorithm.

import jscatter as js
import numpy as np

pQACC = js.formel.pQACC  # shortcut
pQFGxD = js.formel.pQFGxD

def cuboid(q, phi, theta, a, b, c):
    # integrand
    # scattering for orientations phi, theta as 1 dim arrays from 2dim integration
    # q is array for vectorized integration in last dimension
    # basically scheme as q*theta[:,None] results in array output of correct shape
    pi2 = np.pi * 2
    fa = (np.sinc(q * a * np.sin(theta[:,None]) * np.cos(phi[:,None]) / pi2) *
          np.sinc(q * b * np.sin(theta[:,None]) * np.sin(phi[:,None]) / pi2) *
          np.sinc(q * c * np.cos(theta[:,None]) / pi2))
    # add volume, sin(theta) weight of integration, normalise for unit sphere
    return fa**2*(a*b*c)**2*np.sin(theta[:,None])/np.pi/4

q=np.r_[0,0.1:11.1:0.1]
NN=20
a,b,c = 2,2,2

# quadrature: use one quadrant and multiply later by 8
FqCC,err = pQACC(cuboid,[0,0],[np.pi/2,np.pi/2],parnames=['phi','theta'],q=q,a=a,b=b,c=c)
FqGL=js.formel.pQFGxD(cuboid,[0,0],[np.pi/2,np.pi/2],parnames=['phi','theta'],q=q,a=c,b=b,c=c,n=NN)

p=js.grace()
p.multi(2,1)
p[0].title('Comparison adaptive Gauss and Clenshaw-Curtis integration',size=1.2)
p[0].subtitle('Cuboid formfactor integrated over unit sphere')
p[0].plot(q,FqCC*8,sy=1,le='CC')
p[0].plot(q,FqGL*8,sy=0,li=[1,2,4],le='GL')
p[1].plot(q,err,li=[1,2,2],sy=0,le='error estimate CC')
p[1].plot(q,np.abs(FqCC*8-FqGL*8),li=[3,2,4],sy=0,le='difference')
p[0].xaxis(label=r'', min=0, max=15,)
p[1].xaxis(label=r'q / nm\S-1', min=0, max=15)
p[0].yaxis(label='I(q)',scale='log',ticklabel='power')
p[1].yaxis(label='I(q)', scale='log',ticklabel='power', min=1e-16, max=1e-6)
p[1].legend(y=1e-12,x=8)
p[0].legend(y=1,x=12)
#p.save(js.examples.imagepath+'/Clenshaw-Curtis.jpg')

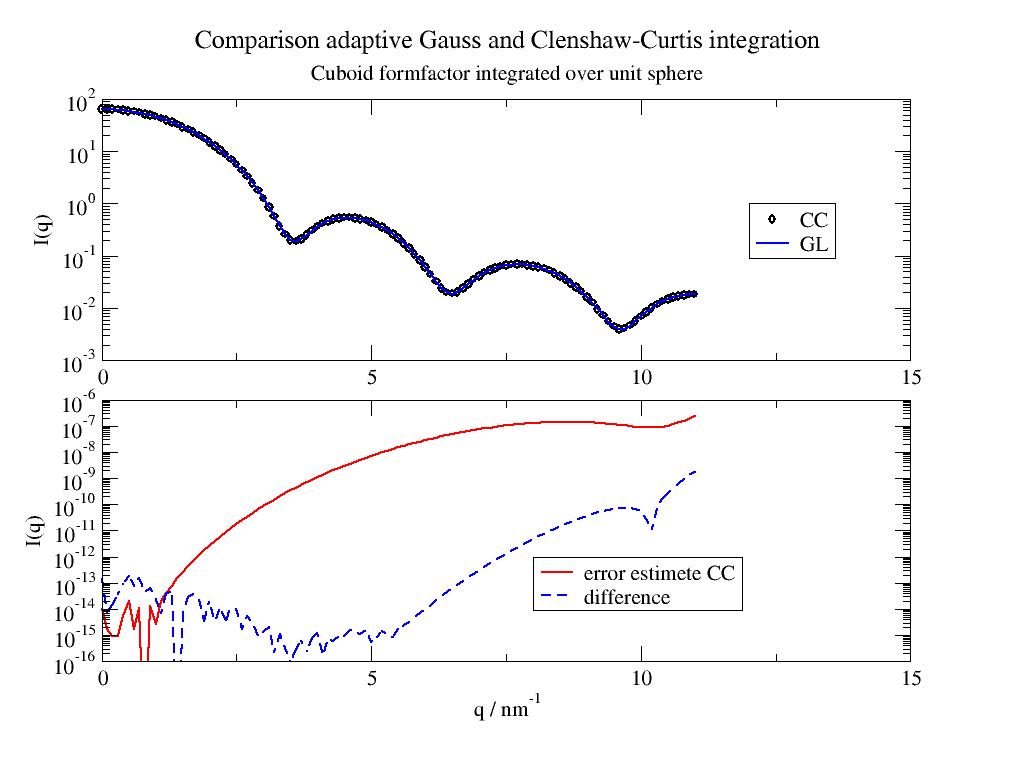
jscatter.formel.quadrature.parQuadratureAdaptiveGauss(func, lowlimit, uplimit, parname, weights=None, tol=1e-08, rtol=1e-08, maxiter=150, miniter=8, **kwargs)[source]¶

Vectorized definite integral using fixed-tolerance Gaussian quadrature. Shortcut pQAG.

parQuadratureAdaptiveClenshawCurtis is more efficient. Adaptive integration of func from a to b using Gaussian quadrature adaptivly increasing number of points by 8. All columns are integrated. For func return values as dataArray the .X is recovered (unscaled) while for array also the X are integrated and weighted.

Parameters:

funcfunction

A function or method to integrate returning an array or dataArray.

lowlimitfloat

Lower limit of integration.

uplimitfloat

Upper limit of integration.

parnamestring

name of the integration variable which should be a scalar.

weightsndarray shape(2,N),default=None

Weights for integration along parname as a Gaussian with lowlimit<weights[0]<uplimit and weights[1] contains weight values.
Missing values are linear interpolated (faster).

If None equal weights=1 are used.

kwargsdict, optional

Extra keyword arguments to pass to function, if any.

tol, rtolfloat, optional

Iteration stops when error between last two iterates is less than tol OR the relative change is less than rtol.

maxiterint, default 150, optional

Maximum order of Gaussian quadrature.

miniterint, default 8, optional

Minimum order of Gaussian quadrature.

ncpuint, default=1, optional

Number of cpus in the pool. Set this to 1 if the integrated function uses multiprocessing to avoid errors.

0 -> all cpus are used

int>0 min (ncpu, mp.cpu_count)

int<0 ncpu not to use

Returns:

valfloat: Gaussian quadrature approximation (within tolerance) to integral for all vector elements.
errfloat: Difference between last two estimates of the integral.

Notes

Reimplementation of scipy.integrate.quadrature.quadrature to work with vector output of the integrand function.

References

[1]

https://en.wikipedia.org/wiki/Gaussian_quadrature

Examples

A simple polydispersity: integrate size distribution of equal weight. Normalisation by 4sig.

We see that Rg and I0 at low Q also change because of polydispersity. Minima are smeared out.

import jscatter as js
q=js.loglist(0.01,5,500)
p=js.grace()
mean=5
for sig in [0.01,0.1,0.3,0.4]:  # distribution width
    sp2=js.formel.pQAG(js.ff.sphere,mean-2*sig,mean+2*sig,'radius',q=q,radius=mean)
    p.plot(sp2.X, sp2.Y/(4*sig),sy=[-1,0.2,-1])
p.yaxis(scale='l')

Integrate Gaussian as test case. As we integrate over .X the final .X will be the first integration point .X, here the first Legendre knot.

t=np.r_[1:100]
gg=js.formel.gauss(t,50,10)
js.formel.pQAG(js.formel.gauss,0,100,'x',mean=50,sigma=10)

jscatter.formel.quadrature.parQuadratureFixedGauss(func, lowlimit, uplimit, parname, n=25, weights=None, **kwargs)[source]¶

Vectorized definite integral using fixed-order Gaussian quadrature. Shortcut pQFG.

Integrate func over parname from lowlimit to uplimit using Gauss-Legendre quadrature [1] of order n. All columns are integrated. For func return values as dataArray the .X is recovered (unscaled) while for array also the X are integrated and weighted.

Parameters:

funccallable

A Python function or method returning a vector array of dimension 1. If func returns dataArray .Y is integrated.

lowlimitfloat

Lower limit of integration.

uplimitfloat

Upper limit of integration.

parnamestring

Name of the integration variable which should be a scalar. After evaluation the corresponding attribute has the mean value with weights.

weightsndarray shape(2,N),default=None

Weights for integration along parname with lowlimit<weights[0]<uplimit and weights[1] as weight values.
Missing values are linear interpolated.

If None equal weights=1 are used. To use normalised weights normalise it or use scipy.stats distributions.

kwargsdict, optional

Extra keyword arguments to pass to function, if any.

nint, optional

Order of quadrature integration. Default is 15.

ncpuint,default=1, optional

Use parallel processing for the function with ncpu parallel processes in the pool. Set this to 1 if the function is already fast enough or if the integrated function uses multiprocessing.

0 -> all cpus are used

int>0 min (ncpu, mp.cpu_count)

int<0 ncpu not to use

Returns:

array or dataArray

Notes

Gauss-Legendre quadrature of function \(f(x,p)\) over parameter \(p\) with a weight function \(v(p)\)

Reimplementation of scipy.integrate.quadrature.fixed_quad to work with vector output of the integrand function and weights.

\(w_i\) and \(p_i\) are the associated weights and knots of the Legendre polynominals.

\[\int_{-1}^1 f(x,p) v(p) dp \approx \sum_{i=1}^n w_i v_i f(x,p_i)\]

Change of interval to [a,b] is done as

\[\int_a^b f(x, p)\,dp = \int_{-1}^1 \left(\frac{b-a}{2}\xi + \frac{a+b}{2}\right) \frac{dx}{d\xi}d\xi\]

with \(\frac{dx}{d\xi} = \frac{b-a}{2}\) .

References

[1]

https://en.wikipedia.org/wiki/Gaussian_quadrature

Examples

A simple polydispersity of spheres: integrate size distribution with weights.

We see that Rg and I0 at low Q also change because of polydispersity. \(I_0~R^6\). Minima are smeared out.

For a Gaussian distribution the edge values are less weighted but broader and the central values are stronger weighted. The effect on I0 is stronger and the minima are more smeared.

The uniform distribution is the same as weights=None, but normalised to 1. Using None we get the same (weight=1) if the result is normalised by the width 2*sig.

import jscatter as js
import scipy
q=js.loglist(0.01,5,500)
p=js.grace()
p.multi(2,1)
mean=5

# use a uniform distribution
for sig in [0.1,0.5,0.8,1]:  # distribution width
    distrib = scipy.stats.uniform(loc=mean-sig,scale=2*sig)
    x = np.r_[mean-3*sig:mean+3*sig:30j]
    pdf = np.c_[x,distrib.pdf(x)].T
    sp2 = js.formel.pQFG(js.ff.sphere,mean-sig,mean+sig,'radius',q=q,radius=mean,n=20, weights=pdf)
    p[0].plot(sp2.X, sp2.Y,sy=[-1,0.2,-1])
p[0].yaxis(label='I(Q)',scale='l')
p[0].xaxis(label=r'')
p[0].text('uniform distribution',x=2,y=1e5)

# use a Gaussian distribution
for sig in [0.1,0.5,0.8,1]:  # distribution width
    distrib = scipy.stats.norm(loc=mean,scale=sig)
    x = np.r_[mean-3*sig:mean+3*sig:30j]
    pdf = np.c_[x,distrib.pdf(x)].T
    sp2 = js.formel.pQFG(js.ff.sphere,mean-2*sig,mean+2*sig,'radius',q=q,radius=mean,n=25,weights=pdf)
    p[1].plot(sp2.X, sp2.Y,sy=[-1,0.2,-1])
p[1].yaxis(label='I(Q)',scale='l')
p[1].xaxis(label=r'Q / nm\S-1')
p[1].text('Gaussian distribution',x=2,y=1e5)

Integrate Gaussian as test case. This is not the intended usage. As we integrate over .X the final .X will be the last integration point .X, here the last Legendre knot. The integral is 1 as the gaussian is normalised.

import jscatter as js
import numpy as np
import scipy
# testcase: integrate over x of a function
# area under normalized gaussian is 1
js.formel.pQFG(js.formel.gauss,-10,10,'x',mean=0,sigma=1)

jscatter.formel.quadrature.parQuadratureFixedGaussxD(func, lowlimit, uplimit, parnames, n=5, weights0=None, weights1=None, weights2=None, **kwargs)[source]¶

Vectorized fixed-order Gauss-Legendre quadrature in definite interval in 1,2,3 dimensions. Shortcut pQFGxD.

Integrate func over parnames between limits using Gauss-Legendre quadrature [1] of order n.

Parameters:

funccallable

Function to integrate. The return value should be 2 dimensional array with first dimension along integration variable and second along array to calculate. See examples.

parnameslist of string, max len=3

Name of the integration variables which should be scalar in the function.

lowlimitlist of float

Lower limits a of integration for parnames.

uplimitlist of float

Upper limits b of integration for parnames.

weights0,weights1,weights3ndarray shape(2,N), default=None

Weights for integration along parname with lowlimit<weightsi<uplimit and weightsi[1] contains weight values.
Missing values are linear interpolated (faster).
None: equal weights=1 are used.

If None equal weights=1 are used. To use normalised weights normalise it or use scipy.stats distributions.

kwargsdict, optional

Extra keyword arguments to pass to function, if any.

nint, optional

Order of quadrature integration for all parnames. Default is 5.

Returns:

array

Notes

To get a speedy integration the function should use numpy ufunctions which operate on numpy arrays with compiled code.

References

[1]

https://en.wikipedia.org/wiki/Gaussian_quadrature

Examples

The following integrals in 1-3 dimensions over a normalised Gaussian give always 1 which achieved with reasonable accuracy with n=15.

The examples show different ways to return 2dim arrays with x,y,z in first dimension and vector q in second. x[:,None] adds a second dimension to array x.

import jscatter as js
import numpy as np
q=np.r_[0.1:5.1:0.1]
def gauss(x,mean,sigma):
   return np.exp(-0.5 * (x - mean) ** 2 / sigma ** 2) / sigma / np.sqrt(2 * np.pi)

# 1dimensional
def gauss1(q,x,mean=0,sigma=1):
    g=np.exp(-0.5 * (x[:,None] - mean) ** 2 / sigma ** 2) / sigma / np.sqrt(2 * np.pi)
    return g*q
js.formel.pQFGxD(gauss1,0,100,parnames='x',mean=50,sigma=10,q=q,n=15)

# 2 dimensional
def gauss2(q,x,y=0,mean=0,sigma=1):
    g=gauss(x[:,None],mean,sigma)*gauss(y[:,None],mean,sigma)
    return g*q
js.formel.pQFGxD(gauss2,[0,0],[100,100],parnames=['x','y'],mean=50,sigma=10,q=q,n=15)

# 3 dimensional
def gauss3(q,x,y=0,z=0,mean=0,sigma=1):
    g=gauss(x,mean,sigma)*gauss(y,mean,sigma)*gauss(z,mean,sigma)
    return g[:,None]*q
js.formel.pQFGxD(gauss3,[0,0,0],[100,100,100],parnames=['x','y','z'],mean=50,sigma=10,q=q,n=15)

Usage of weights allows weights for dimensions e.g. to realise a spherical average with weight \(sin(\theta)d\theta\) in the integral \(P(q) = \int_0^{2\pi}\int_0^{\pi} f(q,\theta,\phi) sin(\theta) d\theta d\phi\). (Using the weight in the function is more accurate.) The weight needs to be normalised by unit sphere area \(4\pi\).

import jscatter as js
import numpy as np
q=np.r_[0,0.1:5.1:0.1]
def cuboid(q, phi, theta, a, b, c):
    pi2 = np.pi * 2
    fa = (np.sinc(q * a * np.sin(theta[:,None]) * np.cos(phi[:,None]) / pi2) *
          np.sinc(q * b * np.sin(theta[:,None]) * np.sin(phi[:,None]) / pi2) *
          np.sinc(q * c * np.cos(theta[:,None]) / pi2))
    return fa**2*(a*b*c)**2

# generate weight for sin(theta) dtheta integration (better to integrate in cuboid function)
# and normalise for unit sphere
t = np.r_[0:np.pi:180j]
wt = np.c_[t,np.sin(t)/np.pi/4].T

Fq=js.formel.pQFGxD(cuboid,[0,0],[2*np.pi,np.pi],parnames=['phi','theta'],weights1=wt,q=q,n=15,a=1.9,b=2,c=2)

# compare the result to the ff solution (which does the same with weights in the function).
p=js.grace()
p.plot(q,Fq)
p.plot(js.ff.cuboid(q,1.9,2,2),li=1,sy=0)
p.yaxis(scale='l')

jscatter.formel.quadrature.parQuadratureSimpson(funktion, lowlimit, uplimit, parname, weights=None, tol=1e-06, rtol=1e-06, dX=None, **kwargs)[source]¶

Vectorized quadrature over one parameter with weights using the adaptive Simpson rule. Shortcut pQS.

Integrate by adaptive Simpson integration for all .X values at once. Only .Y values are integrated and checked for tol criterion. Attributes and non .Y columns correspond to the weighted mean of parname.

Parameters:

funktionfunction

Function returning dataArray or array

lowlimit,uplimitfloat

Interval borders to integrate

parnamestring

Parname to integrate

weightsndarray shape(2,N),default=None

Weights for integration along parname as a Gaussian with a<weights[0]<b and weights[1] contains weight values.
Missing values are linear interpolated (faster). If None equal weights are used.

tol,rtolfloat, default=1e-6

Relative  error or absolute error to stop integration. Stop if one is full filled.
Tol is divided for each new interval that the sum of tol is kept.
.IntegralErr_funktEvaluations in dataArray contains error and number of points in interval.

dXfloat, default=None

Minimal distance between integration points to determine a minimal step for integration variable.

kwargs

Additional parameters to pass to funktion. If parname is in kwargs it is overwritten.

Returns:

dataArray or array: dataArrays have additional parameters as error and weights.

Notes

What is the meaning of tol in Simpson method? If the error in an interval exceeds tol, the algorithm subdivides the interval in two equal parts with each \(tol/2\) and applies the method to each subinterval in a recursive manner. The condition in interval i is \(error=|f(ai,mi)+f(mi,bi)-f(ai,bi)|/15 < tol\). The recursion stops in an interval if the improvement is smaller than tol. Thus tol is the upper estimate for the total error.

Here we use a absolute (tol) and relative (rtol) criterion: \(|f(ai,mi)+f(mi,bi)-f(ai,bi)|/15 < rtol*fnew\) with \(fnew= ( f(ai,mi)+f(mi,bi) + [f(ai,mi)+f(mi,bi)-f(ai,bi)]/15 )\) as the next improved value As this is tested for all .X the worst case is better than tol, rtol.

The algorithm is efficient as it memoizes function evaluation at each interval border and reuses the result. This reduces computing time by about a factor 3-4.

Different distribution can be found in scipy.stats. But any distribution given explicitly can be used. E.g. triangular np.c_[[-1,0,1],[0,1,0]].T

References

[1]

https://en.wikipedia.org/wiki/Adaptive_Simpson’s_method

Examples

Integrate Gaussian as test case. As we integrate over .X the final .X will be the first integration point .X, here the lowlimit.

import jscatter as js
import numpy as np
import scipy
# testcase: integrate over x of a function
# area under normalized gaussian is 1
js.formel.parQuadratureSimpson(js.formel.gauss,-10,10,'x',mean=0,sigma=1)

Integrate a function over one parameter with a weighting function. If weight is 1 the result is a simple integration. Here the weight corresponds to a normal distribution and the result is a weighted average as implemented in parDistributedAverage using fixedGaussian quadrature.

# normal distribtion of parameter D with width ds
t=np.r_[0:150:0.5]
D=0.3
ds=0.1
diff=js.dynamic.simpleDiffusion(t=t,q=0.5,D=D)
distrib =scipy.stats.norm(loc=D,scale=ds)
x=np.r_[D-5*ds:D+5*ds:30j]
pdf=np.c_[x,distrib.pdf(x)].T
diff_g=js.formel.parQuadratureSimpson(js.dynamic.simpleDiffusion,-3*ds+D,3*ds+D,parname='D',
                                         weights=pdf,tol=0.01,q=0.5,t=t)
# compare it
p=js.grace()
p.plot(diff,le='monodisperse')
p.plot(diff_g,le='polydisperse')
p.xaxis(scale='l')
p.legend()

jscatter.formel.quadrature.scatteringFromSizeDistribution(q, sizedistribution, size=None, func=None, weight=None, **kwargs)[source]¶

Average function assuming one multimodal parameter like bimodal.

Distributions might be mixtures of small and large particles bi or multimodal. For predefined distributions see formel.parDistributedAverage with examples. The weighted average over given sizedistribution is calculated.

Parameters:

qarray of float;: Wavevectors to calculate scattering; unit = 1/unit(size distribution)
sizedistributiondataArray or array: Explicit given distribution of sizes as [ [list size],[list probability]]
sizestring: Name of the parameter describing the size (may be also something different than size).
funclambda or function, default beaucage: Function that describes the form factor with first arguments (q,size,…) and should return dataArray with .Y as result as e.g.func=js.ff.sphere.
kwargs: Any additional keyword arguments passed to for func.
weightfunction: Weight function dependent on size. E.g. weight = lambda R:rho**2 * (4/3*np.pi*R**3)**2 with V= 4pi/3 R**3 for normalized form factors to account for forward scattering of volume objects of dimension 3.

Returns:

dataArray: Columns [q,I(q)]

Notes

We have to discriminate between formfactor normalized to 1 (e.g. beaucage) and form factors returning the absolute scattering (e.g. sphere) including the contrast. The later contains already \(\rho^2 V^2\), the first not.

We need for normalized formfactors P(q) \(I(q) = n \rho^2 V^2 P(q)\) with \(n\) as number density \(\rho\) as difference in average scattering length (contrast), V as volume of particle (~r³ ~ mass) and use \(weight = \rho^2 V(R)^2\)

\[I(q)= \sum_{R_i} [ weight(R_i) * probability(R_i) * P(q, R_i , *kwargs).Y ]\]

For a gaussian chain with \(R_g^2=l^2 N^{2\nu}\) and monomer number N (nearly 2D object) we find \(N^2=(R_g/l)^{1/\nu}\) and the forward scattering as weight \(I_0=b^2 N^2=b^2 (R_g/l)^{1/\nu}\)

Examples

The contribution of different simple sizes to Beaucage

import jscatter as js
q=js.loglist(0.01,6,100)
p=js.grace()
# bimodal with equal concentration
bimodal=[[12,70],[1,1]]
Iq=js.formel.scatteringFromSizeDistribution(q=q,sizedistribution=bimodal,
                                            d=3,weight=lambda r:(r/12)**6,func=js.ff.beaucage)
p.plot(Iq,legend='bimodal 1:1 weight ~r\S6 ')
Iq=js.formel.scatteringFromSizeDistribution(q=q,sizedistribution=bimodal,d=3,func=js.ff.beaucage)
p.plot(Iq,legend='bimodal 1:1 weight equal')
# 2:1 concentration
bimodal=[[12,70],[1,5]]
Iq=js.formel.scatteringFromSizeDistribution(q=q,sizedistribution=bimodal,d=2.5,func=js.ff.beaucage)
p.plot(Iq,legend='bimodal 1:5 d=2.5')
p.yaxis(label='I(q)',scale='l')
p.xaxis(scale='l',label='q / nm\S-1')
p.title('Bimodal size distribution Beaucage particle')
p.legend(x=0.2,y=10000)
#p.save(js.examples.imagepath+'/scatteringFromSizeDistribution.jpg')

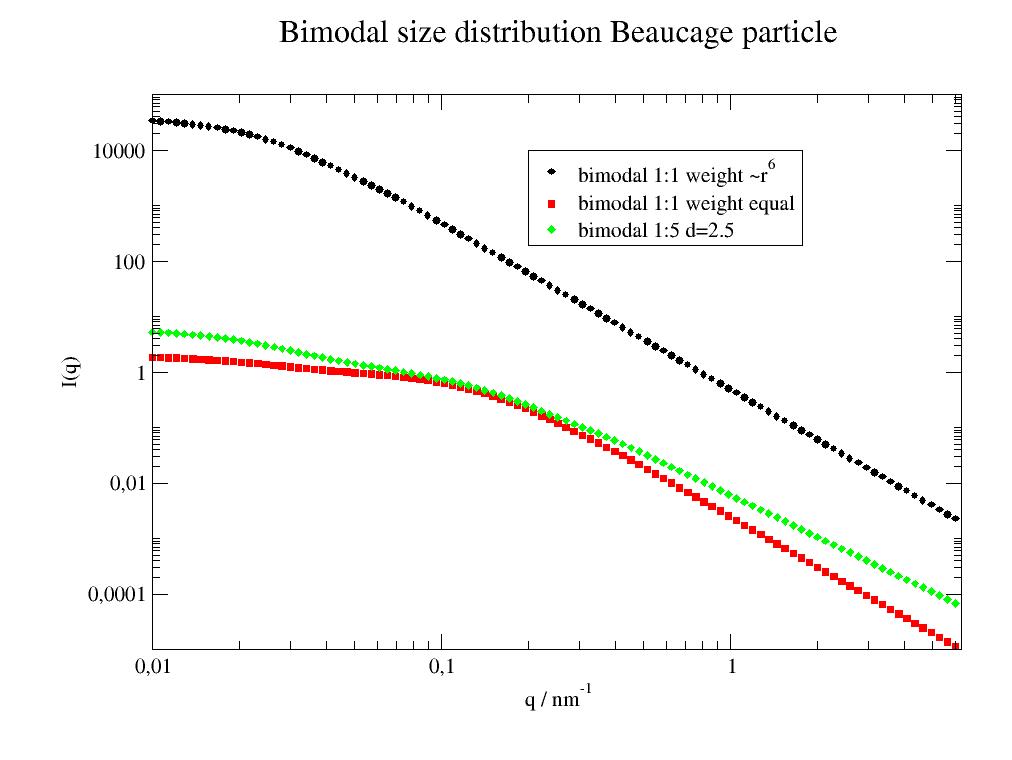
Three sphere sizes:

import jscatter as js
q=js.loglist(0.001,6,1000)
p=js.grace()
# trimodal with equal concentration
trimodal=[[10,50,500],[1,0.01,0.00001]]
Iq=js.formel.scatteringFromSizeDistribution(q=q,sizedistribution=trimodal,size='radius',func=js.ff.sphere)
p.plot(Iq,legend='with aggregates')
p.yaxis(label='I(q)',scale='l',max=1e13,min=1)
p.xaxis(scale='l',label='q / nm\S-1')
p.text(r'minimum \nlargest',x=0.002,y=1e10)
p.text(r'minimum \nmiddle',x=0.02,y=1e7)
p.text(r'minimum \nsmallest',x=0.1,y=1e5)
p.title('trimodal spheres')
p.subtitle('first minima indicated')
#p.save(js.examples.imagepath+'/scatteringFromSizeDistributiontrimodal.jpg')

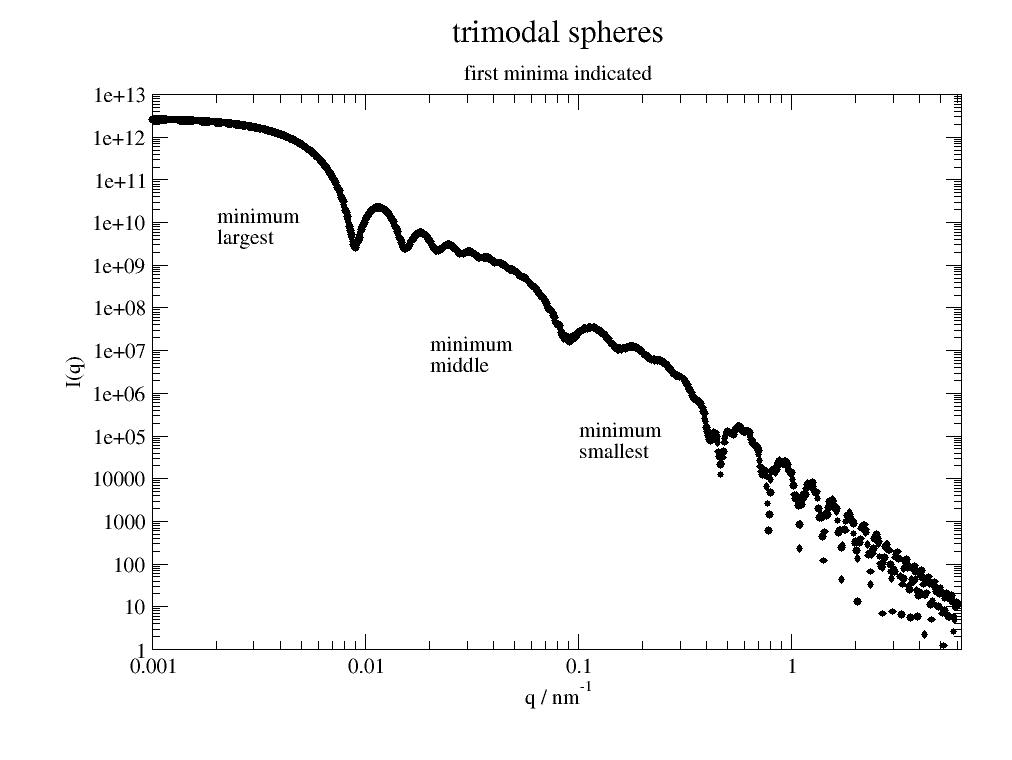
jscatter.formel.quadrature.simpleQuadratureSimpson(funktion, lowlimit, uplimit, parname, weights=None, tol=1e-06, rtol=1e-06, **kwargs)[source]¶

Integrate a scalar function over one of its parameters with weights using the adaptive Simpson rule. Shortcut sQS.

Integrate by adaptive Simpson integration for scalar function.

Parameters:

funktionfunction

function to integrate

lowlimit,uplimitfloat

interval to integrate

parnamestring

parname to integrate

weightsndarray shape(2,N),default=None

Weights for integration along parname as a Gaussian with a<weights[0]<b and weights[1] contains weight values.
Missing values are linear interpolated (faster). If None equal weights are used.

tol,rtolfloat, default=1e-6

Relative error for intervals or absolute integral error to stop integration.

kwargs

additional parameters to pass to funktion if parname is in kwargs it is overwritten

Returns:

float

Notes

What is the meaning of tol in Simpson method? See parQuadratureSimpson.

References

[1]

https://en.wikipedia.org/wiki/Adaptive_Simpson’s_method

Examples

distrib =scipy.stats.norm(loc=1,scale=0.2)
x=np.linspace(0,1,1000)
pdf=np.c_[x,distrib.pdf(x)].T
# define function
f1=lambda x,p1,p2,p3:js.dA(np.c_[x,x*p1+x*x*p2+p3].T)
# calc the weighted integral
result=js.formel.parQuadratureSimpson(f1,0,1,parname='p2',weights=pdf,tol=0.01,p1=1,p3=1e-2,x=x)
# something simple should be 1
js.formel.simpleQuadratureSimpson(js.formel.gauss,-10,10,'x',mean=0,sigma=1)

class jscatter.formel.imageHash(image, type=None, hashsize=8, highfreq_factor=4)[source]¶

Creates image hash of an image to find duplicates or similar images in a fast way using the Hamming difference.

Implements * average hashing (aHash) * perception hashing (pHash) * difference hashing (dHash)

Parameters:

imagefilename, hexstr, PIL image

Image to calculate a hash. If a hexstr is given to restore a saved hash it must prepend ‘0x’ and the 0-padded length determines the hash size. type needs to be given additionally.

type‘ahash’, ‘dhash’, ‘phash’

Hash type.

hashsizeint , default 16

Hash size as hashsize x hashsize array.

highfreq_factorint, default=4

For ‘phash’ increase initial image size to hashsize*highfreq_factor for cos-transform to catch high frequencies.

Returns imageHash object

.bin, .hex, .int return respective representations
.similarity(other) returns relative Hamming distance.
imageHash subtractions returns Hamming distance.
equality checks hashtype and Hamming distance equal zero.

Notes

Images similarity cannot be done by bit comparison (e.g. md5sum) but using a simplified image representation converted to a unique bit representation representing a hash for the image.

Similar images should be different only in some bits measured by the Hamming distance (number of different bits).

A typical procedure is

Reduce color by converting to grayscale.
Reduce size to e.g. 8x8 pixels by averaging over blocks.
Calc binary pixel hash pased on pixel values:

ahash - average hash: hash[i,j] = pixel > average(pixels)

dhash - difference hash: hash[i,j] = pixel[i,j+1] > pixel[i,j]

phash - perceptual hash:
The low frequency part of the image cos-transform are most perceptual. The cos-transform of the image is used for an average hash. hash[i,j] = ahash(cos_tranform(pixels))

radial variance: See radon tranform in [1] (not implemented)

ahash and dhash are faster but phash dicriminates best.
Image similarity is decribed by the Hamming difference as number of different bits. A good measure is the relative Hamming difference (my similarity) as Hamming_diff/hash.size.
Similar images have similarity < 0.1 .
Random pixel difference results in similarity=0.5, an iverted image in similarity =1 (all bits different)

References

[1]

Rihamark: perceptual image hash benchmarking C. Zauner, M. Steinebach, E. Hermann Proc. SPIE 7880, Media Watermarking, Security, and Forensics III https://doi.org/10.1117/12.876617

Started based on photohash and imagehash

Examples

The calibration image migth be not the best choice as demo or a good one. rotate works not at the center of the beam but for the image center.

import jscatter as js
from jscatter.formel import imageHash
from PIL import Image
image = Image.open(js.examples.datapath+'/calibration.tiff')
type='dhash'
original_hash = imageHash(image=image, type=type)
rotate_image = image.rotate(-1) 
rotate_hash = imageHash(image=rotate_image,type=type)
sim1 = original_hash.similarity(rotate_hash)

rotate_image = image.rotate(-90)
rotate_hash = imageHash(image=rotate_image, type=type)
sim2 = original_hash.similarity(rotate_hash)

property bin¶: Binary representation

property hex¶: Hexadecimal representation

property int¶: Integer representation

property shape¶: Shape of the hash.

similarity(other)[source]¶

Relative Hamming difference.

Similar <0.1
Random pixels are close to 0.5
Inverted 1

property size¶: Size of the hash.

Collection of data tables.

jscatter.data.felectron = 2.8179403267e-06¶: electron cross-section

jscatter.data.radiusBohr = 0.0529177210903¶: Bohr radius in unit nm

jscatter.data.xrayFFatomic¶: Dict of atomic xray formfactor for elements as dataArray with [q, coherent, incoherent]

jscatter.data.Elements¶: Elements Dictionary with: { symbol : (e- number; mass; neutron coherent scattering length, neutron incoherent scattering length, name)}; units amu for mass and nm for scattering length

jscatter.data.Nscatlength¶: Dictionary with neutron scattering length for elements as [b_coherent, b_incoherent]. units nm from http://www.ncnr.nist.gov/resources/n-lengths/list.html

jscatter.data.vdwradii¶

jscatter.data.aaHydrophobicity¶: Hydrophobicity of aminoacids Kyte J, Doolittle RF., J Mol Biol. 1982 May 5;157(1):105-32.

Functions for parallel computations on a single multicore machine using the standard library multiprocessing and some related stuff.

jscatter.parallel.doForList(funktion, looplist, *args, **kwargs)[source]¶

Parallel execution of a function in a pool of workers to speed up (multiprocessing).

Apply function with values in looplist in a pool of workers in parallel using multiprocessing. Like multiprocessing map_async but distributes automatically all given arguments.

Parameters:

funktionfunction

Function to process with arguments (args, loopover[i]=looplist[j,i], kwargs) Return value of function should contain parameters or at least the loopover value to allow a check, if desired.

loopoverlist of string, default= None

Names of arguments to use for (sync) looping over with values in looplist.

If not given the first funktion argument is used.
If loopover is single argument this gets looplist[i,:]
Two arguments to loopover : loopover=['q', 'iq']

looplistlist or list of tuples with len(loopover)

List of values to loop over.

single argument just use a list [0.01,0.1,0.2,0.3,0.4]
for above ‘q’, ‘iq’ maybe looplist=[(q, i) for i, q in enumerate([0.01,0.1,0.2,0.3,0.4])]

ncpuint, optional

Number of cpus in the pool if started as main process (otherwise single process).

not given or 0 -> all cpus are used
int>0 min (ncpu, mp.cpu_count)
int<0 ncpu not to use

cbNone, function

Callback after each calculation.

debugint

debug > 0 allows serial output for testing.

outputbool

If False no output is shown.

Returns:

listlist of function return values as [result1,result2,…..]

The order of return values is not explicitly synced to looplist. The return array may be prepended with the value looplist[i] as reference. E.g.:

def f(x,a,b,c,d):
result = x+a+b+c+d
    return [x, result]

Notes

Functions for parallel computations on a single multicore machine using the standard library multiprocessing.

Not the programming details, but the way how to speed up some things.

If your computation is already fast (e.g. <1s) go on without parallelisation. In an optimal case you gain a speedup as the number of cpu cores.
If you want to use a cluster with all cpus, this is not the way (you need MPI).

Parallelisation is no magic and this module is for convenience for non-specialist of parallel computing. The main thing is to pass additional parameters to the processes (a pool of workers) and loop only over one parameter given as list. Opening and closing of the pool is hidden in the function. In this way we can use a multicore machine with all cpus.

During testing, I found that shared memory does not really speed up in most cases, if we just want to calculate a function e.g. for a list of different Q values dependent on model parameters. Here the pickling of numpy arrays is efficient enough compared to the computation we do. The amount of data pickled should not be too large as each process gets a copy and pickling needs time.

If speed is an issue and shared memory gets important i advice using Fortran with OpenMP as used for ff.cloudScattering with parallel computation and shared memory. For me this was easier than the different solutions around.

We use here only non-modified input data and return a new dataset, so we don’t need to care about what happens if one process changes the data needed in another process (race conditions,…), anyway it’s not shared. Please keep this in mind and don’t complain if you find a way to modify input data.

For easier debugging (to find the position of an error in the pdb debugger) use the option debug. In this case the multiprocessing is not used and the debugger finds the error correctly.

Shared memory

Shared memory can be created and used with shared_create() , shared_recover() and shared_close().

See notes and example in shared_create().

Examples

Using in a module This is the prefered and intended way for usage that works on Linux, macOS and also on Windows.

Write a module like the following and name the file myfunctions.py .

import jscatter as js
import numpy as np

def f(x,a,b,c,d):
   res=x+a+b+c+d
   return [x,res]

def f2(x,a,b,c,d):
   res=x[0]+x[1]+a+b+c+d
   return [x[0],res]

def mycomplicatedModel(N,a,b,c,d):
    # using a list of 2 values for x (is first argument)
    loop = np.arange(N).reshape(-1,2)  # has 2 values in second dimension
    res = js.formel.doForList(f2,looplist=loop,a=a,b=b,c=c,d=d)
    return res

Create a working script where you use your functions defined in above module or do this on the command line.

import myfunctions as mf

res = mf.mycomplicatedModel(100,a=1,b=2,c=3,d=11)

Using in a simple script Not recommended! Already repeating is only possible with __spec__=None

This is what you find looking for multiprocessing in Windows as a typical usage pattern This is only neccessary on Windows but not on Linux or macOS

Take the following and paste it to script.py In a python shell do run scripy.py The calculation is encapsulated in the if clause and only executed on the main level. This if line is not needed for Linux or macOS

import jscatter as js
import numpy as np

def f(x,a,b,c,d):
   res=x+a+b+c+d
   return [x,res]

def f2(x,a,b,c,d):
   res=x[0]+x[1]+a+b+c+d
   return [x[0],res]

if __name__ == '__main__':
   __spec__ = None
    # loop over first argument, here x
    res = js.formel.doForList(f,looplist=np.arange(100),a=1,b=2,c=3,d=11)
    # loop over 'd' ignoring the given d=11 (which can be omitted here)
    res = js.formel.doForList(f,looplist=np.arange(100),loopover='d',x=0,a=1,b=2,c=3,d=11)

    # using a list of 2 values for x (is first argument)
    loop = np.arange(100).reshape(-1,2)  # has 2 values fin second dimension
    res = js.formel.doForList(f2,looplist=loop,a=1,b=2,c=3,d=11)

    # looping over several variables in sync
    loop = np.arange(100).reshape(-1,2)
    res = js.formel.doForList(f2,looplist=loop,loopover=['a','b'],x=[100,200],a=1,b=2,c=3,d=11)

jscatter.parallel.fibonacciLatticePointsOnSphere(NN, r=1)[source]¶

Fibonacci lattice points on a sphere with radius r (default r=1)

This can be used to integrate efficiently over a sphere with well distributed points.

Parameters:

NNinteger: number of points = 2*N+1
rfloat, default 1: radius of sphere

Returns:

list of [r,phi,theta] pairs in radians: phi azimuth -pi<phi<pi; theta polar angle 0<theta<pi

References

[1]

Measurement of Areas on a Sphere Using Fibonacci and Latitude–Longitude Lattices Á. González Mathematical Geosciences 42, 49-64 (2009)

Examples

import jscatter as js
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
points=js.formel.fibonacciLatticePointsOnSphere(1000)
pp=list(filter(lambda a:(a[1]>0) & (a[1]<np.pi/2) & (a[2]>0) & (a[2]<np.pi/2),points))
pxyz=js.formel.rphitheta2xyz(pp)
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(pxyz[:,0],pxyz[:,1],pxyz[:,2],color="k",s=20)
ax.set_xlim([-1,1])
ax.set_ylim([-1,1])
ax.set_zlim([-1,1])
plt.tight_layout()
plt.show(block=False)

points=js.formel.fibonacciLatticePointsOnSphere(1000)
pp=list(filter(lambda a:(a[2]>0.3) & (a[2]<1) ,points))
v=js.formel.rphitheta2xyz(pp)
R=js.formel.rotationMatrix([1,0,0],np.deg2rad(30))
pxyz=np.dot(R,v.T).T
#points in polar coordinates
prpt=js.formel.xyz2rphitheta(np.dot(R,pxyz.T).T)
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(pxyz[:,0],pxyz[:,1],pxyz[:,2],color="k",s=20)
ax.set_xlim([-1,1])
ax.set_ylim([-1,1])
ax.set_zlim([-1,1])
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
plt.tight_layout()
plt.show(block=False)

jscatter.parallel.haltonSequence(size, dim, skip=0)[source]¶

Pseudo random numbers from the Halton sequence in interval [0,1].

To use them as coordinate points transpose the array.

Parameters:

sizeint: Samples from the sequence
dimint: Dimensions
skipint: Number of points to skip in Halton sequence .

Returns:

array

Notes

The visual difference between pseudorandom and random in 2D. See [2] for more details.

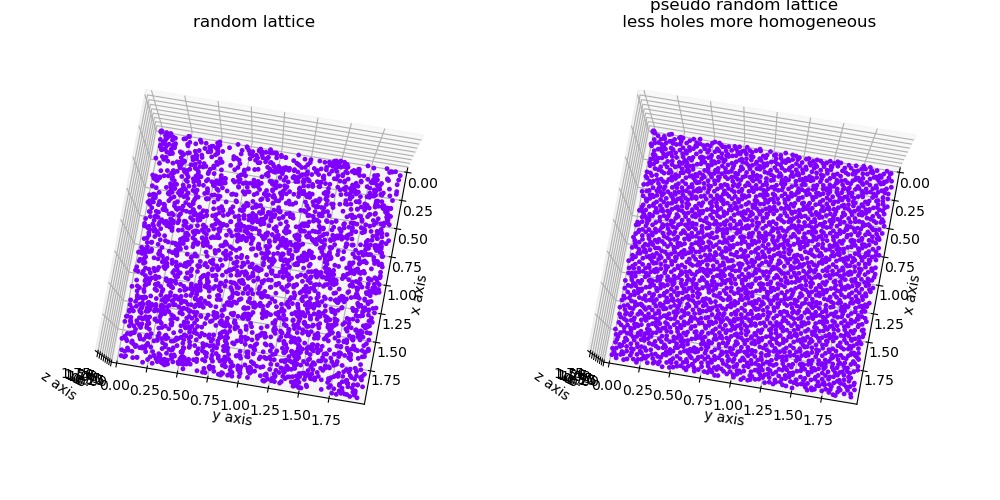
References

[1]

https://mail.python.org/pipermail/scipy-user/2013-June/034741.html Author: Sebastien Paris, Josef Perktold translation from c

[2]

https://en.wikipedia.org/wiki/Low-discrepancy_sequence

Examples

import jscatter as js
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
for i,color in enumerate(['b','g','r','y']):
   # create halton sequence and shift it to needed shape
   pxyz=js.formel.haltonSequence(400,3).T*2-1
   ax.scatter(pxyz[:,0],pxyz[:,1],pxyz[:,2],color=color,s=20)
ax.set_xlim([-1,1])
ax.set_ylim([-1,1])
ax.set_zlim([-1,1])
plt.tight_layout()
plt.show(block=False)

jscatter.parallel.randomPointsInCube(NN, skip=0, dim=3)[source]¶

N quasi random points in cube of edge 1 based on low-discrepancy sequence.

For numerical integration quasi random numbers are better than random samples as the error drops faster [1]. Here we use the Halton sequence to generate the sequence. Skipping points makes the sequence additive and does not repeat points.

Parameters:

NNint: Number of points to generate.
skipint: Number of points to skip in Halton sequence .
dimint, default 3: Dimension of the cube.

Returns:

array of [x,y,z]

References

[1] (1,2)

https://en.wikipedia.org/wiki/Low-discrepancy_sequence

Examples

The visual difference between pseudorandom and random in 2D. See [1] for more details.

import jscatter as js
import matplotlib.pyplot as pyplot
fig = pyplot.figure(figsize=(10, 5))
fig.add_subplot(1, 2, 1, projection='3d')
fig.add_subplot(1, 2, 2, projection='3d')
js.sf.randomLattice([2,2],3000).show(fig=fig, ax=fig.axes[0])
fig.axes[0].set_title('random lattice')
js.sf.pseudoRandomLattice([2,2],3000).show(fig=fig, ax=fig.axes[1])
fig.axes[1].set_title('pseudo random lattice \n less holes more homogeneous')
fig.axes[0].view_init(elev=85, azim=10)
fig.axes[1].view_init(elev=85, azim=10)
#fig.savefig(js.examples.imagepath+'/comparisonRandom-Pseudorandom.jpg')

Random cubes of random points in cube.

# random cubes of random points in cube
import jscatter as js
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
N=30
cubes=js.formel.randomPointsInCube(20)*3
for i,color in enumerate(['b','g','r','y','k']*3):
   points=js.formel.randomPointsInCube(N,skip=N*i).T
   pxyz=points*0.3+cubes[i][:,None]
   ax.scatter(pxyz[0,:],pxyz[1,:],pxyz[2,:],color=color,s=20)
ax.set_xlim([0,3])
ax.set_ylim([0,3])
ax.set_zlim([0,3])
plt.tight_layout()
plt.show(block=False)
#fig.savefig(js.examples.imagepath+'/randomRandomCubes.jpg')

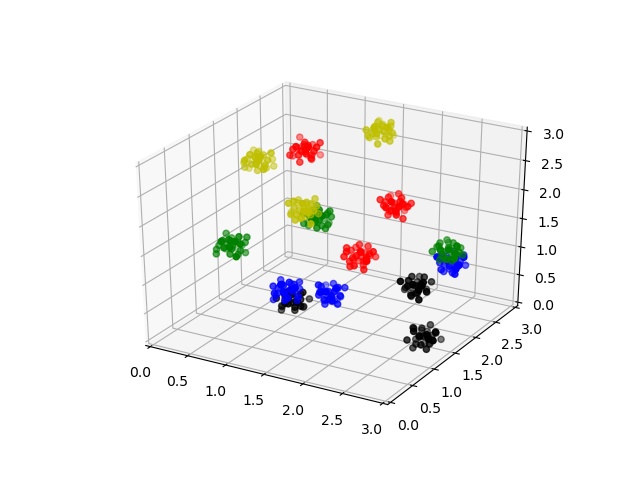
jscatter.parallel.randomPointsOnSphere(NN, r=1, skip=0)[source]¶

N quasi random points on sphere of radius r based on low-discrepancy sequence.

For numerical integration quasi random numbers are better than random samples as the error drops faster [1]. Here we use the Halton sequence to generate the sequence. Skipping points makes the sequence additive and does not repeat points.

Parameters:

NNint: Number of points to generate.
rfloat: Radius of sphere
skipint: Number of points to skip in Halton sequence .

Returns:

array of [r,phi,theta] pairs in radians

References

[1]

https://en.wikipedia.org/wiki/Low-discrepancy_sequence

Examples

A random sequence of points on sphere surface.

import jscatter as js
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
for i,color in enumerate(['b','g','r','y']):
   points=js.formel.randomPointsOnSphere(400,skip=400*i)
   points=points[points[:,1]>0,:]
   pxyz=js.formel.rphitheta2xyz(points)
   ax.scatter(pxyz[:,0],pxyz[:,1],pxyz[:,2],color=color,s=20)
ax.set_xlim([-1,1])
ax.set_ylim([-1,1])
ax.set_zlim([-1,1])
fig.axes[0].set_title('random points on sphere (half shown)')
plt.tight_layout()
plt.show(block=False)
#fig.savefig(js.examples.imagepath+'/randomPointsOnSphere.jpg')

jscatter.parallel.shared_close(shm)[source]¶

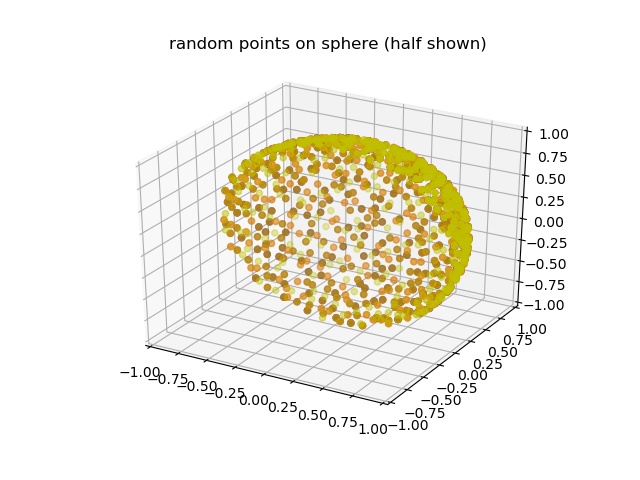
Close and unlink shared memory array.

Parameters:

shmsharedMemory: SharedMemory created by shared_create.

jscatter.parallel.shared_create(ar)[source]¶

Create shared memory array before sending into pool of workers or usage in doForList .

Creation of shared memory for numpy arrays as described in https://docs.python.org/3/library/multiprocessing.shared_memory.html#module-multiprocessing.shared_memory

Parameters:

ararray: Numpy array to copy into a shared memory array.

Returns:

sharedMemory, tuple with (namestring, ar.shape, ar.dtype)

sharedMemory is the shared memory
tuple is information to recover the original array, name is a unique identifier The tuple needs to be passed to the function in doForList instead of ar.

Notes

This function (with shared_recover() and shared_close()) is more for experts.

The speedup e.g. in cloudScattering is not huge as the main time is consumed in calculations.

Also creating shared memory (~8ms for 1e6x3 array) takes around the same time as numpy array pickling (~3ms) for transfer to a pool of workers. Inside the pool the recover is much faster (~ 47µs) compared to unpickling (1.2.ms)

The speedup will be more important if e.g. the qlist (see example) is huge and the calculations are short. In this case data transfer will be more important than the calculation.

Examples

Take the following and paste it to script.py In a python shell do run scripy.py In this way the fucntions are defined and can be accessed.

Using this in imported scripts is not necessary.

import jscatter as js
import numpy as np

def model(q, ar_id):
   # recover the array from shared memory
   ar_sh, ar = js.formel.shared_recover(ar_id)

   # here we do a difficult calculation for a single q value but the whole array
   sum = np.sum(q*ar)
   ar_sh.close()
   return sum

if __name__ == '__main__':
    __spec__ = None
    qlist=np.r_[0.1:10:0.1]

    # example grid with about 1e6 points
    cloud = js.ff.superball(1, 10, p=2, nGrid=100, returngrid=True).XYZ

    # transfer large grid to shared memory
    cloud_sh, cloud_id = js.formel.shared_create(cloud)

    # do the calculation for a qlist values
    res = js.formel.doForList(model, qlist, loopover='q', ar=cloud_id)

    # always free the shared memory (close and unlink)
    js.formel.shared_close(cloud_sh)

jscatter.parallel.shared_recover(shm_id)[source]¶

Recover shared memory array inside a function evaluated in a pool of workers.

Parameters:

shm_idtuple created by shared_create

Returns:

sharedMemory, ndarray

jscatter.parallel.sphereAverage(funktion, relError=300, *args, **kwargs)[source]¶

Vectorized spherical average of funktion, parallel or non-parallel.

A Fibonacci lattice or Monte Carlo integration with pseudo random grid is used.

Parameters:

funktionfunction

Function to evaluate. Funktion first argument gets cartesian coordinate [x,y,z] of point on unit sphere.

relErrorfloat, default 300

Determines how points on sphere are selected

>1 Fibonacci Lattice with relError*2+1 points
0<1 Pseudo random points on sphere (see randomPointsOnSphere).
Stops if relative improvement in mean is less than relError (uses steps of 40 or (20ncpu) new points). Final error is (stddev of N points) /sqrt(N) as for Monte Carlo methods even if it is not a correct 1-sigma error in this case.

This has to be used with care as convergence might be slow if std is intrinsically large in calculated values.

ncpuint, optional

Number of cpus in the pool if started as main process (otherwise single process).

not given or 0 -> default, all cpus are used
int>0 min (ncpu, mp.cpu_count)
int<0 ncpu not to use

Please check if multiprocessing is really useful. For simple calculations it’s faster not to use it (avoiding pickle overhead). The below first example is around 10times faster on a single core (ncpu=1). Think about passPoints.

passPointsbool

If the function accepts a Nx3 array of points these will be passed instead of single points. The function return value should index the points result in axis 0. This might speed up dependent on the function (e.g. formfactor prism) .

Sets ncpu=1 .

arg,kwargs

forwarded to function

Returns:

array

Values from function and appended Monte Carlo error estimates.

If an array of values is returned in function, the result is also an array with double size.

To separate use values, error = res.reshape(2,-1)
If list of array is returned a list is returned with values and error.

Notes

Works also on single core machines and with single process (avoiding creation of a pool of workers).
For integration over a continuous function as a form factor in scattering the random points are not statistically independent. Think of neighbouring points on an isosurface which are correlated and therefore the standard deviation is biased. In this case the Fibonacci lattice is the better choice as the standard deviation in a random sample is not a measure of error but more a measure of the differences on the isosurface.

Examples

Parallel sphere average

Conversion to rpt coordinates and sum results in average value of these coordinate in result. Error of radius is machine precision, phi,theta errors are typical Monte Carlo error

The function should be used in a module to work on Windows. Usage in a module is recomended like demonstarted in doForList()

import jscatter as js
def f(x,r):
   # return a list of values to integrate
   return [js.formel.xyz2rphitheta(x)*r]
val, error = js.formel.sphereAverage(f,relError=500,r=1)
# => [1, 0, pi/2 ]
js.formel.sphereAverage(f,relError=0.01,r=1)

import jscatter as js
import numpy as np

def fp(singlepoint):
   # return a list of values to integrate
   return js.formel.xyz2rphitheta(singlepoint)[1:]
val,error = js.formel.sphereAverage(fp,relError=500).reshape(2,-1)
val,error = js.formel.sphereAverage(fp,relError=0.1).reshape(2,-1)

Pass all points to one process, not parallel.

def fps(allpoints,r):
   res = js.formel.xyz2rphitheta(allpoints)
   return res

val,error = js.formel.sphereAverage(fps,r=1,passPoints=1).reshape(2,-1)

4. formel¶

4.1. Functions¶

4.2. Quadrature¶

4.3. Distribution of parameters¶

4.4. Parallel execution¶

4.5. Utilities¶

4.6. Centrifugation¶

4.7. NMR¶

4.8. Material Data¶

4.9. Constants and Tables¶

Table of Contents

Previous topic

Next topic

This Page