8. dynamic

Models describing dynamic processes mainly for inelastic neutron scattering.

• Models in the time domain have a parameter t for time. -> intermediate scattering function \(I(t,q)\)

• Models in the frequency domain have a parameter w for frequency and _w appended. -> dynamic structure factor \(S(w,q)\)

Models in time domain can be transformed to frequency domain by time2frequencyFF() implementing the Fourier transform \(S(w,q)=F(I(t,q))\).

In time domain the combination of processes \(I_i(t,q)\) is done by multiplication, including instrument resolution \(R(t,q)\):

\(I(t,q)=I_1(t,q)I_2(t,q)R(t,q)\).

# multiplying and creating new dataArray
I(t,q) = js.dA( np.c[t, I1(t,q,..).Y*I2(t,q,..).Y*R(t,q,..).Y ].T)

In frequency domain it is a convolution, including the instrument resolution.

\(S(w,q) = S_1(w,q) \otimes S_2(w,q) \otimes R(w,q)\).

conv=js.formel.convolve
S(w,q)=conv(conv(S1(w,q,..),S2(w,q,..)),res(w,q,..),normB=True)      # normB normalizes resolution

res(w,q,..) might be a measurement or the result of a fit to a measurement. A fitted measurement assumes a continous extrapolation at the edges and a smoothing, while a measurement is cut at the edges to zero and contains noise.

Time to frequency FFT

FFT from time domain by time2frequencyFF() may include the resolution where it acts like a window function to reduce spectral leakage with vanishing values at \(t_{max}\). If not used \(t_{max}\) needs to be large (see tfactor) to reduce spectral leakage.

shiftAndBinning

The last step is to shift the model spectrum to the symmetry point of the instrument as found in the resolution measurement and optional binning over frequency channels. Both is done by shiftAndBinning().

Usage example

Example

Let us describe the diffusion of a particle inside a diffusing invisible sphere by mixing time domain and frequency domain.

resolutionparameter={'s0':5,'m0':0,'a0':1,'bgr':0.00}
w=np.r_[-100:100:0.5]
resolution=js.dynamic.resolution_w(w,**resolutionparameter)
# model
def diffindiffSphere(w,q,R,Dp,Ds,w0,bgr):
    # time domain with transform to frequency domain
    diff_w=js.dynamic.time2frequencyFF(js.dynamic.simpleDiffusion,resolution,q=q,D=Ds)
    # last convolution in frequency domain, resolution is already included in time domain.
    Sx=js.formel.convolve(js.dynamic.diffusionInSphere_w(w=w,q=q,D=Dp,R=R),diff_w)
    Sxsb=js.dynamic.shiftAndBinning(Sx,w=w,w0=w0)
    Sxsb.Y+=bgr       # add background
    return Sxsb
#
Iqw=diffindiffSphere(w=w,q=5.5,R=0.5,Dp=1,Ds=0.035,w0=1,bgr=1e-4)

For more complex systems e.g a number x of diffusing hydrogens and a number y of fixed oxygen and carbons different scattering length and changing fraction of contributing atoms (with scattering length) has to be included just by adding a corresponding factor. This factor can e.g. be determined from an atomic structure.

Accordingly, if desired, the mixture of coherent and incoherent scattering needs to be accounted for by corresponding scattering length. This additionally is dependent on the used instrument e.g. for spin echo only 1/3 of the incoherent scattering contributes to the signal. An example model for protein dynamics is given in Protein incoherent scattering in frequency domain.

A comparison of different dynamic models in frequency domain is given in examples. A comparison of different dynamic models in frequency domain.

For conversion to energy use E = ℏ*w = js.dynamic.hbar*w with h/2π = 4.13566/2π [µeV*ns] = 0.6582 [µeV*ns]

8.1. Transform between domains

time2frequencyFF(timemodel, resolution[, w, ...])	Fast Fourier transform from time domain to frequency domain for inelastic neutron scattering.
shiftAndBinning(data[, w, dw, w0])	Shift spectrum and average (binning) in intervals.

Helpers

getHWHM(data[, center, gap])	Find half width at half maximum (left/right) of a distribution around center.
convolve(A, B[, mode, normA, normB])	Convolve A and B with proper tracking of the output X axis.
dynamicSusceptibility(data, Temp)	Transform from S(w,q) to the imaginary part of the dynamic susceptibility.
h	Planck constant in µeV*ns
hbar	h/2π reduced Planck constant in µeV*ns

8.2. Time domain

resolution(t[, s0, m0, s1, m1, s2, m2, s3, ...])	Resolution in time domain as multiple Gaussians for inelastic measurement as back scattering or time of flight instrument.
simpleDiffusion(t[, gamma, q, D, w, beta, type])	Intermediate scattering function [g1(t)] for diffusing particles from distribution of relaxation rates.
doubleDiffusion(t[, q, gamma1, D1, w1, ...])	Intermediate scattering function [g1(t)] for diffusing particles from bimodal distribution of relaxation rates.
cumulant(x[, k0, k1, k2, k3, k4, k5])	Cumulant of order ki.
cumulantDLS(t, A, G, sigma[, skewness, bgr])	Cumulant analysis for dynamic light scattering assuming Gaussian size distribution.
finiteRouse(t, q[, NN, pmax, l, frict, Dcm, ...])	Rouse dynamics of a finite chain with N beads of bonds length l and internal friction.
finiteZimm(t, q[, NN, pmax, l, Dcm, Dcmfkt, ...])	Zimm dynamics of a finite chain with N beads with internal friction and hydrodynamic interactions.
fixedFiniteRouse(t, q[, NN, pmax, l, frict, ...])	Rouse dynamics of a chain with fixed ends with N beads of bonds length l and internal friction.
fixedFiniteZimm(t, q[, NN, pmax, l, Dcm, ...])	Zimm dynamics of a chain with fixed ends with internal friction and hydrodynamic interactions.
integralZimm(t, q[, Temp, viscosity, amp, ...])	Conformational dynamics of an ideal chain with hydrodynamic interaction, coherent scattering.
stretchedExp(t, gamma, beta[, amp])	Stretched exponential function.
jumpDiffusion(t, Q, t0, l0)	Incoherent intermediate scattering function of translational jump diffusion in the time domain.
methylRotation(t, q[, t0, fraction, rhh, beta])	Incoherent intermediate scattering function of CH3 methyl rotation in the time domain.
diffusionHarmonicPotential(t, q, rmsd, tau)	ISF corresponding to the standard OU process for diffusion in harmonic potential for dimension 1,2,3.
diffusionPeriodicPotential(t, q, u, rt, Dg)	Fractional diffusion of a particle in a periodic potential.
transRotDiffusion(t, q, cloud, Dr[, Dt, lmax])	Translational + rotational diffusion of an object (dummy atoms); dynamic structure factor in time domain.
zilmanGranekBicontinious(t, q, xi, kappa, eta)	Dynamics of bicontinuous micro emulsion phases.
zilmanGranekLamellar(t, q, df, kappa, eta[, ...])	Dynamics of lamellar microemulsion phases.

8.3. Frequency domain

resolution_w(w[, s0, m0, s1, m1, s2, m2, ...])	Resolution as multiple Gaussians for inelastic measurement as backscattering or time of flight instrument in w domain.
elastic_w(w)	Elastic line; dynamic structure factor in w domain.
transDiff_w(w, q, D)	Translational diffusion; dynamic structure factor in w domain.
jumpDiff_w(w, q, t0, r0)	Jump diffusion; dynamic structure factor in w domain.
diffusionHarmonicPotential_w(w, q, tau, rmsd)	Diffusion in a harmonic potential for dimension 1,2,3 (isotropic averaged), dynamic structure factor in w domain.
diffusionInSphere_w(w, q, D, R)	Diffusion inside of a sphere; dynamic structure factor in w domain.
rotDiffusion_w(w, q, cloud, Dr[, lmax])	Rotational diffusion of an object (dummy atoms); dynamic structure factor in w domain.
nSiteJumpDiffusion_w(w, q, N, t0, r0)	Random walk among N equidistant sites (isotropic averaged); dynamic structure factor in w domain.

---

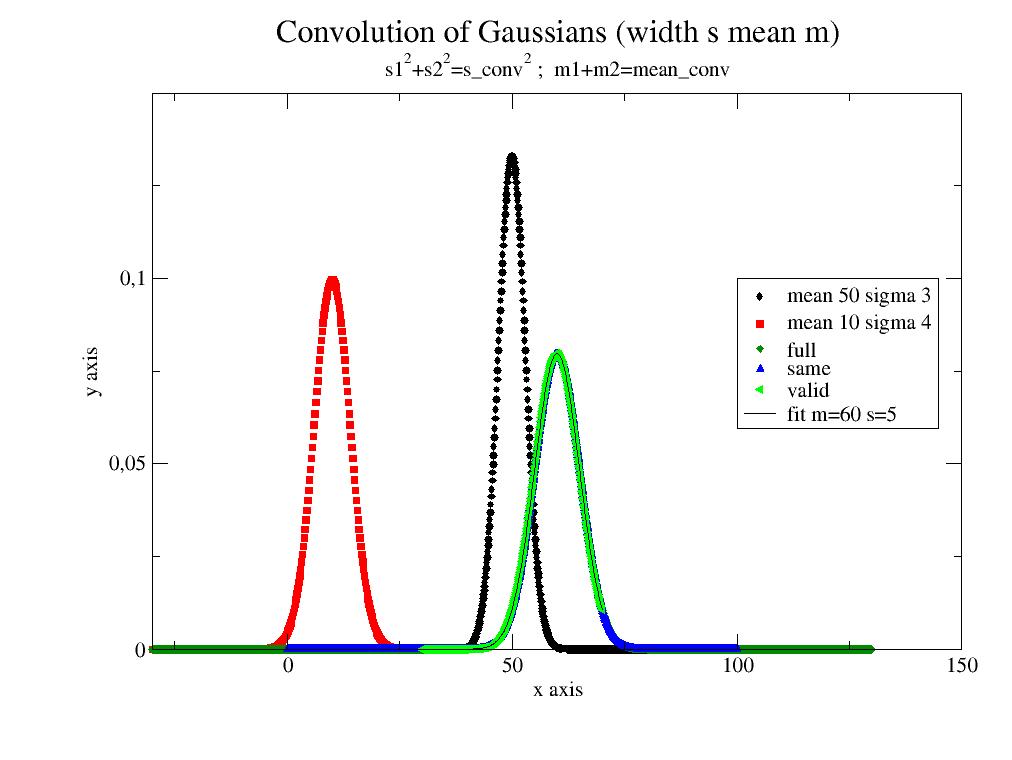
jscatter.dynamic.fft.convolve(A, B, mode='same', normA=False, normB=False)

Convolve A and B with proper tracking of the output X axis.

Approximate the convolution integral as the discrete, linear convolution of two one-dimensional sequences. Missing values are linear interpolated to have matching steps. Values outside of X ranges are set to zero.

Parameters:

A,BdataArray, ndarray

To be convolved arrays (length N and M).

• dataArray convolves Y with Y values

• ndarray A[0,:] is X and A[1,:] is Y

normA,normBbool, default False

Determines if A or B should be normalised that \(\int_{x_{min}}^{x_{max}} A(x) dx = 1\).

mode‘full’,’same’,’valid’, default ‘same’

See example for the difference in range.

• ‘full’ Returns the convolution at each point of overlap,

  with an output shape of (N+M-1,). At the end-points of the convolution, the signals do not overlap completely, and boundary effects may be seen.

• ‘same’ Returns output of length max(M, N).

  Boundary effects are still visible.

• ‘valid’ Returns output of length M-N+1.

Returns:

dataArray

with attributes from A

Notes

• \(A\circledast B (t)= \int_{-\infty}^{\infty} A(x) B(t-x) dx = \int_{x_{min}}^{x_{max}} A(x) B(t-x) dx\)

• If A,B are only 1d array use np.convolve.

• If attributes of B are needed later use .setattr(B,’B-’) to prepend ‘B-’ for B attributes.

References

[1]

Wikipedia, “Convolution”, http://en.wikipedia.org/wiki/Convolution.

Examples

Demonstrate the difference between modes

import jscatter as js;import numpy as np
s1=3;s2=4;m1=50;m2=10
G1=js.formel.gauss(np.r_[0:100.1:0.1],mean=m1,sigma=s1)
G2=js.formel.gauss(np.r_[-30:30.1:0.2],mean=m2,sigma=s2)
p=js.grace()
p.title('Convolution of Gaussians (width s mean m)')
p.subtitle(r's1\S2\N+s2\S2\N=s_conv\S2\N ;  m1+m2=mean_conv')
p.plot(G1,le='mean 50 sigma 3')
p.plot(G2,le='mean 10 sigma 4')
ggf=js.formel.convolve(G1,G2,'full')
p.plot(ggf,le='full')
gg=js.formel.convolve(G1,G2,'same')
p.plot(gg,le='same')
gg=js.formel.convolve(G1,G2,'valid')
p.plot(gg,le='valid')
gg.fit(js.formel.gauss,{'mean':40,'sigma':1},{},{'x':'X'})
p.plot(gg.modelValues(),li=1,sy=0,le='fit m=$mean s=$sigma')
p.legend(x=100,y=0.1)
p.xaxis(max=150,label='x axis')
p.yaxis(min=0,max=0.15,label='y axis')
p.save(js.examples.imagepath+'/convolve.jpg')

jscatter.dynamic.fft.dynamicSusceptibility(data, Temp)

Transform from S(w,q) to the imaginary part of the dynamic susceptibility.

\[ \begin{align}\begin{aligned}\chi (w,q) &= \frac{S(w,q)}{n(w)} (gain side)\\ &= \frac{S(w,q)}{n(w)+1} (loss side)\end{aligned}\end{align} \]

with Bose distribution for integer spin particles

\[with \ n(w)=\frac{1}{e^{hw/kT}-1}\]

Parameters:

datadataArray

Data to transform with w units in 1/ns

Tempfloat

Measurement temperature in K.

Returns:

dataArray

Notes

“Whereas relaxation processes on different time scales are usually hard to identify in S(w,q), they appear as distinct peaks in dynamic susceptibility with associated relaxation times \(\tau ~(2\pi\omega)^{-1}\) [1].

References

[1]

8. Roh et al. ,Biophys. J. 91, 2573 (2006), doi: 10.1529/biophysj.106.082214

Examples

import jscatter as js
import numpy as np
start={'s0':5,'m0':0,'a0':1,'bgr':0.00}
w=np.r_[-100:100:0.2]
resolution=js.dynamic.resolution_w(w,**start)
# model
def diffindiffSphere(w,q,R,Dp,Ds,w0,bgr):
    diff_w=js.dynamic.transDiff_w(w,q,Ds)
    rot_w=js.dynamic.diffusionInSphere_w(w=w,q=q,D=Dp,R=R)
    Sx=js.formel.convolve(rot_w,diff_w)
    Sxsb=js.dynamic.shiftAndBinning(Sx,w=w,w0=w0)
    Sxsb.Y+=bgr       # add background
    return Sxsb
#
q=5.5;R=0.5;Dp=1;Ds=0.035;w0=1;bgr=1e-4
Iqw=diffindiffSphere(w,q,R,Dp,Ds,w0,bgr)
IqwR=js.dynamic.diffusionInSphere_w(w,q,Dp,R)
IqwT=js.dynamic.transDiff_w(w,q,Ds)
Xqw=js.dynamic.dynamicSusceptibility(Iqw,293)
XqwR=js.dynamic.dynamicSusceptibility(IqwR,293)
XqwT=js.dynamic.dynamicSusceptibility(IqwT,293)
p=js.grace()
p.plot(Xqw)
p.plot(XqwR)
p.plot(XqwT)
p.yaxis(scale='l',label='X(w,q) / a.u.',min=1e-7,max=1e-4)
p.xaxis(scale='l',label='w / ns\S-1',min=0.1,max=100)
# p.save(js.examples.imagepath+'/susceptibility.jpg', size=(2,2))

jscatter.dynamic.fft.getHWHM(data, center=0, gap=0)

Find half width at half maximum (left/right) of a distribution around center.

The hwhm is determined from linear spline between Y values to find (Y.max-Y.min)/2 left and right of the max value. Requirement increasing X values and a flat background. If nothing is found an empty list is returned.

For sparse data a fit with a peak function like a Gaussian/Lorezian is prefered.

Parameters:

datadataArray

Distribution

center: float, default=0

Center (symmetry point) of data. If None the position of the maximum is used.

gapfloat, default 0

Exclude values around center as it may contain a singularity. Excludes values within X<= abs(center-gap). The gap should be large enough to reach the baseline on left/right peak side.

Returns:

list of float with hwhm X>0 , X<0 if existing

Examples

import jscatter as js
import numpy as np

x = np.r_[0:10:200j]
data = js.formel.gauss(x,3,0.3)
data.Y += 2
HWHM = js.dynamic.getHWHM(data,3,1.1)
# => (2*np.log(2))**0.5*0.3 = 1.177 * sigma = 0.353

jscatter.dynamic.fft.h = 4.135667696923859

Planck constant in µeV*ns

jscatter.dynamic.fft.hbar = 0.6582119569509066

h/2π reduced Planck constant in µeV*ns

jscatter.dynamic.fft.shiftAndBinning(data, w=None, dw=None, w0=0)

Shift spectrum and average (binning) in intervals.

The intention is to shift spectra and average over intervals. It should be used after convolution with the instrument resolution, when singular values at zero are smeared by resolution.

Parameters:

datadataArray

Data (from model) to be shifted and averaged in intervals to meet experimental data.

warray

New X values (e.g. from experiment). If w is None data.X values are used.

w0float

Shift by w0 that w_new = w_old + w0

dwfloat, default None

Average over intervals between [w[i]-dw,w[i]+dw] to average over a detector pixel width. If None dw is half the interval to neighbouring points. If 0 the value is only linear interpolated to w values and not averaged (about 10 times faster).

Returns:

dataArray

Notes

For averaging over intervals scipy.interpolate.CubicSpline is used with integration in the intervals.

Examples

import jscatter as js
import numpy as np
w = np.r_[-100:100:0.5]
start = {'s0':6,'m0':0,'a0':1,'s1':None,'m1':0,'a1':1,'bgr':0.00}
resolution = js.dynamic.resolution_w(w,**start)
p = js.grace(1,0.6)
p.plot(resolution, le='original')
wnew = np.r_[-100:100:1.5]
p.plot(js.dynamic.shiftAndBinning(resolution,w=wnew,w0=20,dw=0),le='dw=0')
p.plot(js.dynamic.shiftAndBinning(resolution,w=wnew,w0=20,dw=None),le='dw=None')
p.plot(js.dynamic.shiftAndBinning(resolution,w=wnew,w0=20,dw=3),le='dw=3')
p.legend()
p.yaxis(label='S(w) / a.u.')
p.xaxis(label=r'w / ns\S-1')
# p.save(js.examples.imagepath+'/shiftAndBinning.jpg', size=(2,2))

jscatter.dynamic.fft.time2frequencyFF(timemodel, resolution, w=None, tfactor=7, **kwargs)

Fast Fourier transform from time domain to frequency domain for inelastic neutron scattering.

Shortcut t2fFF calls this function.

Parameters:

timemodelfunction, None

Model for I(t,q) in time domain. t in units of ns. The values for t are determined from w as \(t=[0..n_{max}]\Delta t\) with \(\Delta t=1/max(|w|)\) and \(n_{max}=w_{max}/\sigma_{min} tfactor\). \(\sigma_{min}\) is the minimal width of the Gaussians given in resolution. If None a constant function (elastic scattering) is used.

resolutiondataArray, float, string

dataArray that describes the resolution function as multiple Gaussians (use resolution_w). A nonzero bgr in resolution is ignored and needs to be added afterwards.

• floatvalue is used as width of a single Gaussian in units 1/ns (w is needed below).

  Resolution width is in the range of 6 1/ns (IN5 TOF) to 1 1/ns (Spheres BS).

• string : no resolution (‘elastic’)

warray

Frequencies for the result, e.g. from experimental data. If w is None the frequencies resolution.X are used. This allows to use the fit of a resolution to be used with same w values.

kwargskeyword args

Additional keyword arguments that are passed to timemodel.

tfactorfloat, default 7

Factor to determine max time for timemodel to minimize spectral leakage. tmax=1/(min(resolution_width)*tfactor) determines the resolution to decay as \(e^{-tfactor^2/2}\). The time step is dt=1/max(|w|). A minimum of len(w) steps is used (which might increase tmax). Increase tfactor if artifacts (wobbling) from the limited time window are visible as the limited time interval acts like a window function (box) for the Fourier transform.

Returns:

dataArrayA symmetric spectrum of the Fourier transform is returned.

.Sq \(\rightarrow S(q)=\int_{-\omega_{min}}^{\omega_{max}} S(Q,\omega)d\omega \approx \int_{-\infty}^{\infty} S(Q,\omega)d\omega = I(q,t=0)\)

Integration is done by a cubic spline in w domain on the ‘raw’ fourier transform of timemodel.

.Iqt timemodel(t,kwargs) dataArray as returned from timemodel.

Implicitly this is the Fourier transform to time domain after a successful fit in w domain. Using a heuristic model in time domain as multiple Gaussians or stretched exponential allows a convenient transform to time domain of experimental data.

Notes

We use Fourier transform with real signals. The transform is defined as

\[F(f(t)) = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{\infty} f(t) e^{-i\omega t} dt\]

\[F(f(w)) = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{\infty} f(\omega) e^{i\omega t} d\omega\]

The resolution function is defined as (see resolution_w)

\[ \begin{align}\begin{aligned}\begin{split}R_w(w,m_i,s_i,a_i)&= \sum_i a_i e^{-\frac{1}{2}(\frac{w-m_i}{s_i})^2} = F(R_t(t)) \\\end{split}\\&=\frac{1}{\sqrt{2\pi}} \int_{-\infty}^{\infty} \sum_i{a_i s_i e^{-\frac{1}{2}s_i^2t^2}} e^{-i\omega t} dt\end{aligned}\end{align} \]

using the resolution in time domain with same coefficients \(R_t(t,m_i,s_i,a_i)=\sum_i a_i s_i e^{-\frac{1}{2}s_i^2 t^2}\)

The Fourier transform of a timemodel I(q,t) is

\[I(q,w) = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{\infty} I(q,t) e^{-i\omega t} dt\]

The integral is calculated by Fast Fourier transform as

\[I(q,m\Delta w) = \frac{1}{\sqrt{2\pi}} \Delta t \sum_{n=-N}^{N} I(q,n\Delta t) e^{-i mn/N}\]

\(t_{max}=tfactor/min(s_i)\). Due to the cutoff at \(t_{max}\) a wobbling might appear indicating spectral leakage. Spectral leakage results from the cutoff, which can be described as multiplication with a box function. The corresponding Fourier Transform of the box is a sinc function visible in the frequency spectrum as wobbling. If the resolution is included in time domain, it acts like a window function to reduce spectral leakage with vanishing values at \(t_{max}=N\Delta t\). The second possibility (default) is to increase \(t_{max}\) (increase tfactor) to make the sinc sharp and with low wobbling amplitude.

Mixed domain models

Associativity and Convolution theorem allow to mix models from frequency domain and time domain. After transformation to frequency domain the w domain models have to be convoluted with the FFT transformed model.

Examples

Other usage example with a comparison of w domain and transformed from time domain can be found in A comparison of different dynamic models in frequency domain or in the example of diffusionHarmonicPotential_w().

Compare transDiffusion transform from time domain with direct convolution in w domain.

import jscatter as js
import numpy as np
w=np.r_[-100:100:0.5]
start={'s0':6,'m0':0,'a0':1,'s1':None,'m1':0,'a1':1,'bgr':0.00}
resolution=js.dynamic.resolution_w(w,**start)
p=js.grace(1,1)
D=0.035;qq=3  # diffusion coefficient of protein alcohol dehydrogenase (140 kDa) is 0.035 nm**2/ns
p.title('Inelastic spectrum IN5 like')
p.subtitle(r'resolution width about 6 ns\S-1\N, Q=%.2g nm\S-1\N' %(qq))
# compare diffusion with convolution and transform from time domain
diff_ffw=js.dynamic.time2frequencyFF(js.dynamic.simpleDiffusion,resolution,q=qq,D=D)
diff_w=js.dynamic.transDiff_w(w, q=qq, D=D)
p.plot(diff_w,sy=0,li=[1,3,3],le=r'diffusion D=%.3g nm\S2\N/ns' %(D))
p.plot(diff_ffw,sy=[2,0.3,2],le='fft from time domain')
p.plot(diff_ffw.X,diff_ffw.Y+diff_ffw.Y.max()*1e-3,sy=[2,0.3,7],le=r'fft from time domain with bgr')
# resolution has to be normalized in convolve
diff_cw=js.dynamic.convolve(diff_w,resolution,normB=1)
p.plot(diff_cw,sy=0,li=[1,3,4],le='after convolution in w domain')
p.plot(resolution.X,resolution.Y/resolution.integral,sy=0,li=[1,1,1],le='resolution')
p.yaxis(min=1e-6,max=5,scale='l',label='S(Q,w)')
p.xaxis(min=-100,max=100,label='w / ns\S-1')
p.legend(x=10,y=4)
p.text(string=r'convolution edge ==>\nmake broader and cut',x=10,y=8e-6)
# p.save(js.examples.imagepath+'/dynamic_t2f_examples.jpg', size=(2,2))

Compare the resolutions direct and from transform from time domain.

p=js.grace()
fwres=js.dynamic.time2frequencyFF(None,resolution)
p.plot(fwres,le='fft only resolution')
p.plot(resolution,sy=0,li=2,le='original resolution')

Compare diffusionHarmonicPotential to show simple usage

import jscatter as js
import numpy as np
t2f=js.dynamic.time2frequencyFF
dHP=js.dynamic.diffusionHarmonicPotential
w=np.r_[-100:100]
ql=np.r_[1:14.1:6j]
iqw=js.dL([js.dynamic.diffusionHarmonicPotential_w(w=w,q=q,tau=0.14,rmsd=0.34,ndim=3) for q in ql])
# To move spectral leakage out of our window we increase w and interpolate.
# The needed factor (here 23) depends on the quality of your data and background contribution.
iqt=js.dL([t2f(dHP,'elastic',w=w*13,q=q, rmsd=0.34, tau=0.14 ,ndim=3,tfactor=14).interpolate(w) for q in ql])

p=js.grace()
p.multi(2,3)
p[1].title('Comparison direct and FFT  for ndim= 3')
for i,(iw,it) in enumerate(zip(iqw,iqt)):
    p[i].plot(iw,li=1,sy=0,le='q=$wavevector nm\S-1')
    p[i].plot(it,li=2,sy=0)
    p[i].yaxis(min=1e-5,max=2,scale='log')
    if i in [1,2,4,5]:p[i].yaxis(ticklabel=0)
    p[i].legend(x=5,y=1, charsize=0.7)

jscatter.dynamic.timedomain.cumulant(x, k0=1, k1=0, k2=0, k3=0, k4=0, k5=0)

Cumulant of order ki.

\[I(x) = k_0 exp(-k_1x+1/2k_2x^2-1/6 k_3x^3+1/24k_4x^4-1/120k_5x^5)\]

Cumulants can only be used in initial slope analysis and not for a full fit of DLS data to long times. It is necessary to cut large x

Parameters:

xfloat

Wavevector

k0,k1, k2,k3,k4,k5float

Cumulant coefficients; units 1/x

• k0 amplitude

• k1 expected value

• k2 variance with \(\sqrt(k2/k1) =\) relative standard deviation

• higher order see Wikipedia

Returns:

dataArray

Examples

import jscatter as js
import numpy as np

t = js.loglist(1e-6,10,1000) # in seconds

p=js.grace()
p.xaxis(scale='log')

k1=1/0.001
for f in [0,0.1,10.5]:
   cum=js.dynamic.cumulant(t,k1=k1,k2=f*2*k1)
   p.plot(cum,sy=0,li=-1)

jscatter.dynamic.timedomain.cumulantDLS(t, A, G, sigma, skewness=0, bgr=0.0)

Cumulant analysis for dynamic light scattering assuming Gaussian size distribution.

See Frisken et al [1] :

\[I(t,q) = A exp(-t/G) \big( 1+(sigma/G t)^2/2. - (skewness/G t)^3/6. \big) + bgr\]

Parameters:

tarray

Time

Afloat

Amplitude at t=0; Intercept

Gfloat

Mean relaxation time as 1/decay rate in units of t.

sigmafloat

• relative standard deviation if a gaussian distribution is assumed

• should be smaller 1 or the Taylor expansion is not valid

• k2=variance=sigma**2/G**2

skewnessfloat,default 0

Relative skewness k3=skewness**3/G**3

bgrfloat; default 0

Constant background

Returns:

dataArray

References

[1]

Revisiting the method of cumulants for the analysis of dynamic light-scattering data Barbara J. Frisken APPLIED OPTICS 40, 4087 (2001)

jscatter.dynamic.timedomain.diffusionHarmonicPotential(t, q, rmsd, tau, beta=0, ndim=3)

ISF corresponding to the standard OU process for diffusion in harmonic potential for dimension 1,2,3.

The intermediate scattering function corresponding to the standard OU process for diffusion in an harmonic potential [1]. It is used for localized translational motion in incoherent neutron scattering [2] as improvement for the diffusion in a sphere model. Atomic motion may be restricted to ndim=1,2,3 dimensions and are isotropic averaged. The correlation is assumed to be exponential decaying.

Parameters:

tarray

Time values in units ns

qfloat

Wavevector in unit 1/nm

rmsdfloat

Root mean square displacement <u**2>**0.5 in potential in units nm. <u**2>**0.5 is the width of the potential According to [2] 5*u**2=R**2 compared to the diffusion in a sphere.

taufloat

Correlation time \(\tau_0\) in units ns. Diffusion constant in sphere Ds=u**2/tau

betafloat, default 0

Exponent in correlation function \(\rho(t)\).

• beta=0 : \(\rho(t) = exp(-t/\tau_0)\) normal liquids where memory effects are presumably weak or negligible [2].

• 0<beta,inf : \(\rho(t,beta) = (1+\frac{t}{\beta\tau_0})^{-\beta}\). See [2] equ. 21a. supercooled liquids or polymers, where memory effects may be important correlation functions with slower decay rates should be introduced [2]. See [2] equ. 21b.

ndim1,2,3, default=3

Dimensionality of the diffusion potential.

Returns:

dataArray

Notes

We use equ. 18-20 from [2] and correlation time \(\tau_0\) with equal amplitudes \(u\) in the dimensions as

3 dim case:

\[I_s(Q,t) = e^{-Q^2\langle u^2_x \rangle (1-\rho(t))}\]

2 dim case:

\[I_s(Q,t) = \frac{\pi^{0.5}}{2} e^{-g^2(t)} \frac{erfi(g(t))}{g(t)} \ with \ g(t) = \sqrt{Q^2\langle u^2_x \rangle (1-\rho(t))}\]

1 dim case:

\[I_s(Q,t) = \frac{\pi^{0.5}}{2} \frac{erf(g(t))}{g(t)} \ with \ g(t) = \sqrt{Q^2\langle u^2_x \rangle (1-\rho(t))}\]

with erf as the error function and erfi is the imaginary error function erf(iz)/i

References

[1]

Quasielastic neutron scattering and relaxation processes in proteins: analytical and simulation-based models G. R. Kneller Phys. ChemChemPhys. ,2005, 7,2641–2655

[2] (1,2,3,4,5,6,7)

Gaussian model for localized translational motion: Application to incoherent neutron scattering F. Volino, J.-C. Perrin and S. Lyonnard, J. Phys. Chem. B 110, 11217–11223 (2006)

Examples

import numpy as np
import jscatter as js
t=np.r_[0.1:6:0.1]
p=js.grace(1,1)
p.plot(js.dynamic.diffusionHarmonicPotential(t,1,2,1,1),le='1D ')
p.plot(js.dynamic.diffusionHarmonicPotential(t,1,2,1,2),le='2D ')
p.plot(js.dynamic.diffusionHarmonicPotential(t,1,2,1,3),le='3D ')
p.legend()
p.yaxis(label='I(Q,t)')
p.xaxis(label='Q / ns')
p.subtitle('Figure 2 of ref Volino J. Phys. Chem. B 110, 11217')
# p.save(js.examples.imagepath+'/diffusionHarmonicPotential_t.jpg', size=(2,2))

jscatter.dynamic.timedomain.diffusionPeriodicPotential(t, q, u, rt, Dg, gamma=1)

Fractional diffusion of a particle in a periodic potential.

The diffusion describes a fast dynamics inside of the potential trap with a mean square displacement before a jump and a fractional long time diffusion. For fractional coefficient gamma=1 normal diffusion is recovered.

Parameters:

tarray

Time points, units ns.

qfloat

Wavevector, units 1/nm

ufloat

Root mean square displacement in the trap, units nm.

rtfloat

Relaxation time of fast dynamics in the trap; units ns ( = 1/lambda in [1] )

gammafloat

Fractional exponent gamma=1 is normal diffusion

Dgfloat

Long time fractional diffusion coefficient; units nm**2/ns.

Returns:

dataArray

[t, Iqt , Iqt_diff, Iqt_trap]

Notes

We use equ. 4 of [1] for fractional diffusion coefficient \(D_{\gamma}\) with fraction \(\gamma\) as

\[I(Q,t) = exp(-\frac{1}{6}Q^2 msd(t))\]

\[msd(t) = \langle (x(t)-x(0))^2 \rangle = 6\Gamma^{-1}(\gamma+1)D_{\gamma}t^{\gamma} + 6\langle u^2 \rangle (1-E_{\gamma}(-(\lambda t)^{\gamma}))\]

with the Mittag Leffler function \(E_{\gamma}(-at^{\gamma})\) and Gamma function \(\Gamma\) and \(\lambda =1/r_t\).

The first term in msd describes the long time fractional diffusion while the second describes the additional mean-square displacement inside the trap \(\langle u^2 \rangle\).

For \(\gamma=1 \to E_{\gamma}(-at^{\gamma}) \to exp(-at)\) simplifying the equation to normal diffusion with traps.

References

[1] (1,2,3)

Gupta, S.; Biehl, R.; Sill, C.; Allgaier, J.; Sharp, M.; Ohl, M.; Richter, D. Macromolecules 49 (5), 1941 (2016). https://doi.org/10.1021/acs.macromol.5b02281

Examples

Example similar to protein diffusion in a mesh of high molecular weight PEG as found in [1].

import jscatter as js
import numpy as np
t=js.loglist(0.1,50,100)
p=js.grace()
for i,q in enumerate(np.r_[0.1:2:0.3],1):
    iq=js.dynamic.diffusionPeriodicPotential(t,q,0.5,5,0.036)
    p.plot(iq,symbol=[1,0.3,i],legend='q=$wavevector')
    p.plot(iq.X,iq._Iqt_diff,sy=0,li=[1,0.5,i])
p.title('Diffusion in periodic potential traps')
p.subtitle('lines show long time diffusion contribution')
p.yaxis(max=1,min=1e-2,scale='log',label='I(Q,t)/I(Q,0)')
p.xaxis(min=0,max=50,label='t / ns')
p.legend(x=110,y=0.8)
# p.save(js.examples.imagepath+'/fractalDiff.jpg')

jscatter.dynamic.timedomain.doubleDiffusion(t, q=None, gamma1=None, D1=None, w1=0, gamma2=None, D2=None, w2=0, frac=0.5, beta=1, type='lognorm')

Intermediate scattering function [g1(t)] for diffusing particles from bimodal distribution of relaxation rates.

\[I_i(q,t,D_i,\sigma_i ) = \int g(\Gamma_i, \Gamma_{i,0} \sigma_i ) e^{-\Gamma_i t} d\Gamma_i\]

\[I(q,t) = beta [f\ I_1(q,t,D_i,\sigma_i ) + (1-f)\ I_2(q,t,D_2,\sigma_2 )]\]

and relaxation rates \(\Gamma_{i,0}=q^2D_i\).

Parameters:

tfloat, array

Times

gamma1,gamma2float

Mean relaxation rates in inverse t units. Overrides q and D if given. If q and D given gamma=q*q*D

qfloat, array

Wavevector

betafloat

Intercept \(\beta\) in DLS. The amplitude prefactor.

D1,D2float

Mean diffusion coefficients.

w1,w2float

Relative standard deviations of the diffusion coefficient distributions. In absolute units \(\sigma=w*q^2*D\). For a typical DLS experiment w≈0.25 just from instrument noise (e.g. noise ≈ 1e-3 Zetasizer Nano, Malvern)

type‘truncnorm’, default ‘lognorm’

Distribution shape.

• ‘lognorm’ lognorm distribution as normal distribution on a log scale.

  \[g(x, \mu, \sigma) = \frac{ 1 }{\ x\sigma\sqrt{2\pi}} exp(-\frac{\ln(x- \mu)^2}{ 2 \sigma^2 })\]

• ‘truncnorm’ normal distribution cut at zero.

\[g(x, \mu, \sigma)= e^{-0.5(\frac{x-\mu}{\sigma})^2} / (\sigma\sqrt{2\pi}) \ \text{ for x>0}\]

Returns:

outdataArray

intermediate scattering function or \(g_1\)

• .D1, .D2, .wavevector, .beta respective input parameters

• pdf1, pdf2 : Probability of the distribution in the interval around pdf[0,i] (half distance to neighboring points) that sum(pdf[2])==1 similar to CONTIN results.

Notes

Units of q, t and D result in unit-less [q*q*D*t] like q in 1/cm, t in s -> D in cm*cm/s .

Examples

import jscatter as js
import numpy as np

t = js.loglist(1e-6,10,1000) # in seconds
# ≈ a protein with a MW of 140kDa
D1 = 3e-8  # unit cm^2/s
D2 = 3e-5  # unit cm^2/s
q = 4*np.pi/633e-7*np.sin(np.pi/4)  # 90º HeNe laser in DLS

p=js.grace(1.8,1)
p.multi(1,2)
p[0].xaxis(label=r't / s ',scale='log')
p[0].yaxis(label=r'g\s1\N(t) ')
p[1].xaxis(label=r'\xG\f{} / 1/s ',scale='log')
p[1].yaxis(label=[r'P(\xG\f{})',1,'opposite'],)

for c,w in enumerate([0.25,0.5,1,2],1):
   dls = js.dynamic.doubleDiffusion(t=t,q=q,D1=D1,w1=w,D2=D2,w2=w,frac=0.4)
   p[0].plot(dls,sy=0,li=[1,3,c],le=f'w={w}')
   p[1].plot(dls.pdf1[0], 20 * dls.pdf1[1],sy=0,li=[1,3,c])
   p[1].plot(dls.pdf2[0], 20 * dls.pdf2[1],sy=0,li=[1,3,c])

p[0].legend(x=0.01,y=0.8)
p[0].title('DLS correlation')
p[1].title('rate distribution')
# p.save(js.examples.imagepath+'/doubleDiffusion.jpg',size=(1.8,1))

jscatter.dynamic.timedomain.finiteRouse(t, q, NN=None, pmax=None, l=None, frict=None, Dcm=None, Wl4=None, Dcmfkt=None, tintern=0.0, Temp=293, ftype=None, specm=None, specb=None, rk=None)

Rouse dynamics of a finite chain with N beads of bonds length l and internal friction.

The Rouse model describes the conformational dynamics of an ideal chain. The single chain diffusion is represented by Brownian motion of beads connected by harmonic springs. No excluded volume, random thermal force, drag force with solvent, no hydrodynamic interaction and optional internal friction. Coherent + incoherent scattering.

Parameters:

tarray

Time in units nanoseconds

qfloat, list

Scattering vector, units nm^-1 For a list a dataList is returned otherwise a dataArray is returned

NNinteger

Number of chain beads.

lfloat, default 1

Bond length between beads; unit nm.

pmaxinteger, list of floats

• integer => maximum mode number (\(a_p=1\))

• list => \(a_p\) list of amplitudes>0 for individual modes to allow weighing; not given modes have weight zero

frictfloat

Friction of a single bead/monomer in units Pas*m=kg/s=1e-6 g/ns \(\xi = 6\pi\eta l\), . A monomer bead with l=R=0.1nm = 0.1e-9m in H2O(20°C) (1 mPas) => 1.89e-12 Pas*m. Rouse dynamics in a melt needs the bead friction with effective viscosity of the melt.

Wl4float

\(W_l^4\) Characteristic value to calc friction and Dcm.

\(D_{cm}=\frac{W_l^4}{3R_e^2}\) and characteristic Rouse variable \(\Omega_Rt=(q^2/6)^2 W_l^4 t\)

Dcmfloat

Center of mass diffusion in nm^2/ns.

• \(D_{cm}=k_bT/(N\xi)\) with \(\xi\) = friction of single bead in solvent

• \(D_{cm}=W_l^4/(3Nl^2)=W_l^4/(3Re^2)\)

Dcmfktarray 2xN, function

Function f(q) or array with [qi, f(qi) ] as correction for Dcm like Diff = Dcm*f(q). e.g. for inclusion of structure factor or hydrodynamic function with f(q)=H(Q)/S(q). Missing values are interpolated. Only array input can be pickled to speedup by using formel.memoize .

tinternfloat>0

Relaxation time due to internal friction between neighbouring beads in ns.

ftype‘rni’, ‘rap’,’nonspec’, ‘specrif’, ‘crif’, default = ‘rif’

Type of internal friction. See [7] for a description and respective references.

• ‘rif’: Internal friction between neighboring beads in chain. \(t_{rp}=t_r p^{-2}+t_{intern}\)

• ‘rni’: Rouse model with non-local interactions (RNI). Additional friction between random close approaching beads. \(t_{rp}=t_r p^{-2}+N/p t_{intern}\)

• ‘rap’: Rouse model with anharmonic potentials due to stiffness of the chain \(t_{rp}=t_r p^{-2}+t_{intern}ln(N/p\pi)\)

• ‘specrif’: Specific interactions of strength \(b\) between beads separated by m bonds. See [7]. \(t_{rp}=t_r p^{-2} (1+bm^2)^{-1} + (1+m^2/(1+bm^2))t_{intern}\)

• ‘crif’: Bead confining potential with internal friction. The beads are confined in an additional harmonic potential with \(\frac{1}{2}k_c(r_n-0)^2\) leading to a more compact configuration. \(rk= k_c/k\) describes the relative strength compared to the force between beads \(k\).

Tempfloat

Temperature Kelvin = 273+T[°C]

specm,specb: float

Parameters m, b used in internal friction models ‘spec’ and ‘specrif’.

rkNone , float

\(rk= k_c/k\) describes the relative force constant for ftype ‘crif’.

Returns:

dataArrayfor single q

dataListmultiple q

• [time; Sqt; Sqt_inf; Sqtinc]

• time units ns

• Sqt is coherent scattering with diffusion and mode contributions

• Sqt_inf is coherent scattering with ONLY diffusion

• Sqtinc is incoherent scattering with diffusion and mode contributions (no separate diffusion)

• .q wavevector

• .Wl4

• .Re end to end distance \(R_e^2=l^2N\)

• .trouse rotational correlation time or rouse time

  \(tr_1 = \xi N^2 l^2/(3 \pi^2 k_bT)= <R_e^2>/(3\pi D_{cm}) = N^2\xi/(pi^2k)\)

• .tintern relaxation time due to internal friction

• .tr_p characteristic times \(tr_p=tr_1 p^{-2}+t_{intern}\)

• .beadfriction

• .ftype type of internal friction

• …. use .attr to see all attributes

Notes

The Rouse model describes beads connected by harmonic springs without hydrodynamic interactions and open ends. The coherent intermediate scattering function \(S(q,t)/S(q,0)\) is [1] [2] :

\[\frac{S(q,t)}{S(q,0)} = \frac{1}{N} e^{-q^2D_{cm}t} \sum_{n,m}^N e^{-\frac{1}{6}q^2B(n,m,t)}\]

\[B(n,m,t)=|n-m|^{2\mu}l^2 + \sum_{p=1}^{N-1} A_p cos(\pi pn/N)cos(\pi pm/N) (1-e^{-t/t_{rp}})\]

and for incoherent intermediate scattering function the same with \(n=m\) in the first sum.

with

• \(A_p = a_p\frac{4R_e^2}{\pi^2}\frac{1}{p^2}\) mode amplitude (usual \(a_p=1\))

• \(t_{rp} = \frac{t_r}{p^2}\) mode relaxation time with Rouse time \(t_r =\frac{\xi N R_e^2 }{3\pi^2 k_bT} = \frac{R_e^2}{3\pi^2 D_{cm}} = \frac{N^2 \xi}{\pi^2 k}\)

• \(D_{cm}=kT/{N\xi}\) center of mass diffusion

• \(k=3k_bT/l^2\) force constant k between beads.

• \(\xi=6\pi visc R\) single bead friction \(\xi\) in solvent (e.g. surrounding melt)

• \(t_{intern}=\xi_i/k\) additional relaxation time due to internal friction \(\xi_i\)

Modifications (ftype) for internal friction and additional interaction (see [7] and [9]):

• RIFRouse with internal friction between neighboring beads in chain [3] [4].

  • \(t_{rp}=t_r p^{-2}+t_{intern}\)

  • \(\xi_i=t_{intern}k=t_{intern}3k_bT/l^2\) internal friction per bead

• RNIRouse model with non-local interactions as additional friction between spatial close beads [5] .

  • \(t_{rp}=t_r p^{-2}+Nt_{intern}/p\)

• RAPRouse model with anharmonic potentials in bonds describing the stiffness of the chain [6].

  • \(t_{rp}=t_r p^{-2}+t_{intern}ln(N/p\pi)\)

• SPECRIFSpecific interactions of relative strength \(b\) between beads separated by m bonds.

  Internal friction between neighboring beads as in RIF is added.

  • \(t_{rp}=t_r p^{-2} (1+bm^2)^{-1} + (1+\frac{m^2}{1+bm^2})t_{intern}\)

  • \(b=k_{specific}/k_{neighbor}\) relative strength of both interactions.

  • The interaction is between all pairs separated by m.

• CRIFCompacted Rouse with internal friction [9].

  The beads are confined in an additional harmonic potential with \(\frac{1}{2}k_c(r_n-0)^2\) leading to a more compact configuration. \(rk= k_c/k\) describes the relative strength compared to the force between beads \(k\). Typically \(rk << 1\) .

  • The mode amplitude prefactor changes from Rouse type to modified confined amplitudes

    \[A_p =\frac{4R_e^2}{\pi^2}\frac{1}{p^2}\Rightarrow A_p^c = \frac{4R_e^2}{\pi^2}\frac{1}{\frac{N^2k_c}{\pi^2k}+p^2}\]

  • The mode relaxation time changes from Rouse type to modified confined

    \[t_{rp} = \frac{t_r}{p^2} \Rightarrow t_{rp}^c = \frac{t_r}{\frac{N^2k_c}{\pi^2k} + p^2}\]

  • \(R_e\) allows to determine \(k_c/k\) from small angle scattering data

    \[R_e^2 = \frac{2l^2}{\sqrt{k_c/k}}tanh(\frac{N}{2}\sqrt{k_c/k})\]

  • We assume here that the additional potential is \(\frac{1}{2}k_c(r_n-r_0)^2\) with \(r_0\) as the polymer center of mass. As the Langevin equation only depends on relative distances the internal motions are not affected. The center of mass diffusion \(D_{cm}=f(R_e)\) is not affected as the mode dependent friction coefficients don’t change [9].

  • With \(rk=k_c/k \rightarrow 0\) the original Rouse is recovered for amplitudes, relaxation and \(R_e\) .

A combination of different effects is possible [7] (but not implemented).

The amplitude \(A_p\) allows for additional suppression of specific modes e.g. by topological constraints (see [8]).

From above the triple Dcm,l,NN are fixed.

• If 2 are given 3rd is calculated

• If all 3 are given the given values are used

For an example see example_Zimm.

References

[1]

Doi Edwards Theory of Polymer dynamics in the appendix the equation is found

[2]

Nonflexible Coils in Solution: A Neutron Spin-Echo Investigation of Alkyl-Substituted Polynorbonenes in Tetrahydrofuran Michael Monkenbusch et al.Macromolecules 2006, 39, 9473-9479 The exponential is missing a “t” http://dx.doi.org/10.1021/ma0618979

about internal friction

[3]

Exploring the role of internal friction in the dynamics of unfolded proteins using simple polymer models Cheng et al.JOURNAL OF CHEMICAL PHYSICS 138, 074112 (2013) http://dx.doi.org/10.1063/1.4792206

[4]

Rouse Model with Internal Friction: A Coarse Grained Framework for Single Biopolymer Dynamics Khatri, McLeish| Macromolecules 2007, 40, 6770-6777 http://dx.doi.org/10.1021/ma071175x

[5]

Origin of internal viscosities in dilute polymer solutions P. G. de Gennes J. Chem. Phys. 66, 5825 (1977); https://doi.org/10.1063/1.433861

[6]

Microscopic theory of polymer internal viscosity: Mode coupling approximation for the Rouse model. Adelman, S. A., & Freed, K. F. (1977). The Journal of Chemical Physics, 67(4), 1380–1393. https://doi.org/10.1063/1.435011

[7] (1,2,3,4)

Internal friction in an intrinsically disordered protein - Comparing Rouse-like models with experiments A. Soranno, F. Zosel, H. Hofmann J. Chem. Phys. 148, 123326 (2018) http://aip.scitation.org/doi/10.1063/1.5009286

[8]

Onset of topological constraints in polymer melts: A mode analysis by neutron spin echo spectroscopy D. Richter, L. Willner, A. Zirkel, B. Farago, L. J. Fetters, and J. S. Huang Phys. Rev. Lett. 71, 4158 https://doi.org/10.1103/PhysRevLett.71.4158

[9] (1,2,3)

Looping dynamics of a flexible chain with internal friction at different degrees of compactness. Samanta, N., & Chakrabarti, R. (2015). Physica A: Statistical Mechanics and Its Applications, 436, 377–386. https://doi.org/10.1016/j.physa.2015.05.042

Examples

Coherent and incoherent contributions to Rouse dynamics. To mix the individual q dependent contributions have to be weighted with the according formfactor respectivly incoherent scattering length and instrument specific measurement technique.

import jscatter as js
import numpy as np
t = js.loglist(0.02, 100, 40)
q=np.r_[0.1:2:0.2]
l=0.38  # nm , bond length amino acids
rr = js.dynamic.finiteRouse(t, q, 124, 7, l=0.38, Dcm=0.37, tintern=0., Temp=273 + 60)
p=js.grace()
p.multi(2,1)
p[0].xaxis(scale='log')
p[0].yaxis(label='I(q,t)\scoherent')
p[1].xaxis(label=r't / ns',scale='log')
p[1].yaxis(label=r'I(q,t)\sincoherent')
p[0].title('Rouse dynamics in a solvent')
for i, z in enumerate(rr, 1):
    p[0].plot(z.X, z.Y, line=[1, 1, i], symbol=0, legend='q=%g' % z.q)
    p[0].plot(z.X, z._Sqt_inf, line=[3, 2, i], symbol=0, legend='q=%g diff' % z.q)
    p[1].plot(z.X, z._Sqtinc, line=[1, 2, i], symbol=0, legend='q=%g diff' % z.q)

#p.save(js.examples.imagepath+'/Rousecohinc.jpg')

jscatter.dynamic.timedomain.finiteZimm(t, q, NN=None, pmax=None, l=None, Dcm=None, Dcmfkt=None, tintern=0.0, mu=0.5, viscosity=1.0, ftype=None, rk=None, Temp=293)

Zimm dynamics of a finite chain with N beads with internal friction and hydrodynamic interactions.

The Zimm model describes the conformational dynamics of an ideal chain with hydrodynamic interaction between beads. The single chain diffusion is represented by Brownian motion of beads connected by harmonic springs. Coherent + incoherent scattering.

Parameters:

tarray

Time in units nanoseconds.

q: float, array

Scattering vector in units nm^-1. If q is list a dataList is returned otherwise a dataArray is returned.

NNinteger

Number of chain beads. If not given calculated from Dcm,l, mu.

lfloat, default 1

Bond length between beads; units nm. If not given calculated from Dcm, NN, mu .

pmaxinteger, list of float, default is NN

• integer => maximum mode number taken into account.

• list => list of amplitudes \(a_p > 0\) for individual modes to allow weighing. Not given modes have weight zero.

Dcmfloat

Center of mass diffusion in nm²/ns if explicitly is given. If not given Dcm is calculated

• \(=0.196 k_bT/(R_e visc)\) for theta solvent with \(\mu=0.5\)

• \(=0.203 k_bT/(R_e visc)\) for good solvent with \(\mu=0.6\)

with \(R_e=lN^{\mu}\) .

Dcmfktarray 2xN, function

Function f(q) or array with [qi, f(qi)] as correction for Dcm like Diff = Dcm*f(q). e.g. for inclusion of structure factor and hydrodynamic function with f(q)=H(Q)/S(q). Missing values are interpolated. Only array input can be pickled to speedup by using formel.memoize .

tinternfloat>0

Additional relaxation time due to internal friction between neighbouring beads in units ns.

mufloat in range [0.01,0.99]

\(\mu\) describes solvent quality.

• <0.5 collapsed chain

• =0.5 theta solvent 0.5 (gaussian chain)

• =0.6 good solvent

• >0.6 swollen chain

viscosityfloat

\(\eta\) in units cPoise=mPa*s e.g. water \(visc(T=293 K) =1 mPas\)

Tempfloat, default 273+20

Temperature in Kelvin.

ftype‘czif’, default = ‘zif’

Type of internal friction and interaction modification.

• Default Zimm is used with \(t_{intern}=0\)

• ‘zif’ Internal friction between neighboring beads in chain [3].

  \(t_{zp}=t_z p^{-3\mu}+t_{intern}\)

• ‘czif’ Bead confining harmonic potential with internal friction, only for \(\mu=0.5\) [6] .

  The beads are confined in an additional harmonic potential with \(\frac{1}{2}k_c(r_n-0)^2\) leading to a more compact configuration. \(rk= k_c/k\) describes the relative strength compared to the force between beads \(k\).

rkNone , float

\(rk= k_c/k\) describes the relative force constant for ftype ‘czif’.

Returns:

dataArrayfor single q

dataListfor multiple q

• [time; Sqt; Sqt_inf; Sqtinc; Sqtz]

• time units ns

• Sqt is coherent scattering with diffusion and mode contributions

• Sqt_inf is coherent scattering with ONLY diffusion (no internal modes)

• Sqtinc is incoherent scattering with diffusion and mode contributions (no separate diffusion)

• Sqtz is coherent scattering with diffusion and mode contributions, but no Dcmfkt => f(q)=1

• .q wavevector

• .modecontribution \(a_p\) of coherent modes i in sequence as in PRL 71, 4158 equ (3)

• .Re

• .tzimm => Zimm time or rotational correlation time

• .t_p characteristic times

• …. use .attr for all attributes

Notes

The Zimm model describes beads connected by harmonic springs with hydrodynamic interaction and free ends. The \(\mu\) parameter scales between theta solvent \(\mu=0.5\) and good solvent \(\mu=0.6\) (excluded volume or swollen chain). The coherent intermediate scattering function \(S(q,t)/S(q,0)\) is

\[\frac{S(q,t)}{S(q,0)} = \frac{1}{N} e^{-q^2D_{cm}t}\sum_{n,m}^N e^{-\frac{1}{6}q^2B(n,m,t)}\]

\[B(n,m,t)=|n-m|^{2\mu}l^2 + \sum_{p=1}^{N-1} A_p cos(\pi pn/N)cos(\pi pm/N) (1-e^{-t/t_{zp}})\]

and for incoherent intermediate scattering function the same with \(n=m\) in the first sum.

with

• \(A_p = a_p\frac{4R_e^2}{\pi^2}\frac{1}{p^{2\mu+1}}\) mode amplitude (usual \(a_p=1\))

• \(t_{zp} = t_z p^{-3\mu}\) mode relaxation time

• \(t_z = \eta R_e^3/(\sqrt(3\pi) k_bT)\) Zimm mode relaxation time

• \(R_e=l N^{\mu}\) end to end distance

• \(k=3kT/l^2\) force constant between beads

• \(\xi=6\pi\eta l\) single bead friction in solvent with viscosity \(\eta\)

• \(a_p\) additional amplitude for suppression of specific modes e.g. by topological constraints (see [5]).

• \(D_{cm} = \frac{8}{3(6\pi^3)^{1/2}} \frac{k_bT}{\eta R_e} = 0.196 \frac{k_bT}{\eta R_e}\)

Modifications (ftype) for internal friction and additional interaction:

• ZIFZimm with internal friction between neighboring beads in chain [3] [4].

  • \(t_{zp}=t_z p^{{-3\mu}}+t_{intern}\)

  • \(\xi_i=t_{intern}k=t_{intern}3k_bT/l^2\) internal friction per bead

• CZIFCompacted Zimm with internal friction [6].

  Restricted to \(\mu=0.5\) , a combination with excluded volume is not valid. In [9]_ the beads are confined in an additional harmonic potential around the origin with \(\frac{1}{2}k_c(r_n-0)^2\) leading to a more compact configuration. \(rk= k_c/k\) describes the relative strength compared to the force between beads \(k\). Typically \(rk << 1\) .

  • The mode amplitude prefactor changes from Zimm type to modified confined amplitudes

    \[A_p =\frac{4Nl^2}{\pi^2}\frac{1}{p^2}\Rightarrow A_p^c = \frac{4Nl^2}{\pi^2}\frac{1}{\frac{N^2k_c}{\pi^2k}+p^2}\]

  • The mode relaxation time changes from Zimm type to modified confined with \(t_{z} = \frac{\eta N^{3/2} l^3}{\sqrt(3\pi) k_bT}\)

    \[t_{zp} = t_z \frac{1}{p^{3/2}} \Rightarrow t_{zp}^c = t_z \frac{p^{1/2}}{\frac{N^2k_c}{\pi^2k} + p^2}\]

  • \(R_e^c\) allows to determine \(k_c/k\) from small angle scattering data

    \[(R_e^c)^2 = \frac{2l^2}{\sqrt{k_c/k}}tanh(\frac{N}{2}\sqrt{k_c/k})\]

  • For a free diffusing chain we assume here (not given in [9]_ ) that the additional potential is \(\frac{1}{2}k_c(r_n-r_0)^2\) with \(r_0\) as the polymer center of mass. As the Langevin equation only depends on position distances the internal motions are not affected. The center of mass diffusion \(D_{cm}\) can be calculated similar to the Zimm \(D_{cm}\) in [1] assuming a Gaussian configuration with width \(R_e\). We find

    \[D_{cm} = \frac{kT}{\xi_{p=0}} = \frac{8}{3(6\pi^3)^{1/2}} \frac{kT}{\eta R_e}\]

  • With \(rk=k_c/k \rightarrow 0\) the original Zimm is recovered for amplitudes, relaxation and \(R_e\) .

From above the triple Dcm,l,N are fixed.

• If 2 are given 3rd is calculated.

• If all 3 are given the given values are used.

For an example see example_Zimm.

References

[1]

Doi Edwards Theory of Polymer dynamics in appendix the equation is found

[2]

Nonflexible Coils in Solution: A Neutron Spin-Echo Investigation of Alkyl-Substituted Polynorbonenes in Tetrahydrofuran Michael Monkenbusch et al.Macromolecules 2006, 39, 9473-9479 The exponential is missing a “t” http://dx.doi.org/10.1021/ma0618979

about internal friction

[3] (1,2)

Exploring the role of internal friction in the dynamics of unfolded proteins using simple polymer models Cheng et al.JOURNAL OF CHEMICAL PHYSICS 138, 074112 (2013) http://dx.doi.org/10.1063/1.4792206

[4]

Rouse Model with Internal Friction: A Coarse Grained Framework for Single Biopolymer Dynamics Khatri, McLeish| Macromolecules 2007, 40, 6770-6777 http://dx.doi.org/10.1021/ma071175x

mode contribution factors from

[5]

Onset of Topological Constraints in Polymer Melts: A Mode Analysis by Neutron Spin Echo Spectroscopy D. Richter et al.PRL 71,4158-4161 (1993)

[6] (1,2)

Looping dynamics of a flexible chain with internal friction at different degrees of compactness. Samanta, N., & Chakrabarti, R. (2015). Physica A: Statistical Mechanics and Its Applications, 436, 377–386. https://doi.org/10.1016/j.physa.2015.05.042

Examples

Coherent and incoherent contributions to Zimm dynamics. To mix the individual q dependent contributions of coherent and incoherent these have to be weighted by the according formfactor respectively incoherent scattering length and instrument specific measurement technique. Typically diffusion and mode contributions cannot be separated. At larger Q the diffusion contributes marginally while at low Q diffusion dominates.

import jscatter as js
import numpy as np
t = js.loglist(0.02, 100, 40)
q=np.r_[0.1:2:0.2]
l=0.38  # nm , bond length amino acids
zz = js.dynamic.finiteZimm(t, q, 124, 7, l=0.38, Dcm=0.37, tintern=0., Temp=273 + 60)
p=js.grace(2,2)
p.multi(2,1)
p[0].xaxis(scale='log')
p[0].yaxis(label='I(q,t)\scoherent')
p[1].xaxis(label=r't / ns',scale='log')
p[1].yaxis(label=r'I(q,t)\sincoherent')
p[0].title('Zimm dynamics in a solvent')
for i, z in enumerate(zz, 1):
    p[0].plot(z.X, z.Y, line=[1, 1, i], symbol=0, legend='')
    p[0].plot(z.X, z._Sqt_inf, line=[3, 2, i], symbol=0, legend='')
    p[1].plot(z.X, z._Sqtinc, line=[1, 2, i], symbol=0, legend=f'q={z.q:.1f} nm\\S-1')
p[1].legend(x=0.02,y=0.8,charsize=0.5)
p[0].text('only diffusion', x=0.02,y=0.55)
p[0].text('diffusion + modes', x=15,y=0.65,rot=305)

# p.save(js.examples.imagepath+'/Zimmcohinc.jpg',size=(1,1))

jscatter.dynamic.timedomain.fixedFiniteRouse(t, q, NN=None, pmax=None, l=None, frict=None, Dcm=None, Wl4=None, Dcmfkt=None, tintern=0.0, Temp=293, ftype=None, specm=None, specb=None, rk=None, fixedends=1)

Rouse dynamics of a chain with fixed ends with N beads of bonds length l and internal friction.

Opposite to the finiteRouse() here one or both ends are fixed. This might be a chain tethered to a particle that defines the diffusion. Chains are non interacting.

Parameters:

fixedends0,1,2, default = 1

Number of fixed ends. 0 is only for comparison and corresponds to finiteZimm() .

tarray

Time in units nanoseconds

qfloat, list

Scattering vector, units nm^-1 For a list a dataList is returned otherwise a dataArray is returned

NNinteger

Number of chain beads.

lfloat, default 1

Bond length between beads; unit nm.

pmaxinteger, list of floats

• integer => maximum mode number (\(a_p=1\))

• list => \(a_p\) list of amplitudes>0 for individual modes to allow weighing; not given modes have weight zero

frictfloat

Friction of a single bead/monomer in units Pas*m=kg/s=1e-6 g/ns\(\xi = 6\pi\eta l\), .

A monomer bead with l=R=0.1nm = 0.1e-9m in H2O(20°C) (1 mPas) => 1.89e-12 Pas*m.

Rouse dynamics in a melt needs the bead friction with effective viscosity of the melt which should be much higher than water. Polymer melts are typically examined above the glass temperature of the polymer.

Wl4float

\(W_l^4\) Characteristic value to calc friction and Dcm.

\(\Omega_Rt=(q^2/6)^2 W_l^4 t\)

Dcmfloat

Center of mass diffusion in nm^2/ns.

Dcmfktarray 2xN, function

Function f(q) or array with [qi, f(qi) ] as correction for Dcm like Diff = Dcm*f(q). e.g. for inclusion of structure factor or hydrodynamic function with f(q)=H(Q)/S(q). Missing values are interpolated. Only array input can be pickled to speedup by using formel.memoize .

tinternfloat>0

Relaxation time due to internal friction between neighbouring beads in ns.

ftype‘rni’, ‘rap’,’nonspec’, ‘specrif’, ‘crif’, default = ‘rif’

Type of internal friction. See [7] for a description and respective references.

• ‘rif’: Internal friction between neighboring beads in chain. \(t_{rp}=t_r p^{-2}+t_{intern}\)

• ‘rni’: Rouse model with non-local interactions (RNI). Additional friction between random close approaching beads. \(t_{rp}=t_r p^{-2}+N/p t_{intern}\)

• ‘rap’: Rouse model with anharmonic potentials due to stiffness of the chain \(t_{rp}=t_r p^{-2}+t_{intern}ln(N/p\pi)\)

• ‘specrif’: Specific interactions of strength \(b\) between beads separated by m bonds. See [7]. \(t_{rp}=t_r p^{-2} (1+bm^2)^{-1} + (1+m^2/(1+bm^2))t_{intern}\)

• ‘crif’: Bead confining potential with internal friction. The beads are confined in an additional harmonic potential with \(\frac{1}{2}k_c(r_n-0)^2\) leading to a more compact configuration. \(rk= k_c/k\) describes the relative strength compared to the force between beads \(k\).

Tempfloat

Temperature Kelvin = 273+T[°C]

specm,specb: float

Parameters m, b used in internal friction models ‘spec’ and ‘specrif’.

rkNone , float

\(rk= k_c/k\) describes the relative force constant for ftype ‘crif’.

Returns:

dataArrayfor single q

dataListmultiple q

• [time; Sqt; Sqt_inf; Sqtinc]

• time units ns

• Sqt is coherent scattering with diffusion and mode contributions

• Sqt_inf is coherent scattering with ONLY diffusion

• Sqtinc is incoherent scattering with diffusion and mode contributions (no separate diffusion)

• .q wavevector

• .Wl4

• .Re end to end distance \(R_e^2=l^2N\)

• .trouse rotational correlation time or rouse time

  \(tr_1 = \xi N^2 l^2/(3 \pi^2 k_bT)= <R_e^2>/(3\pi D_{cm}) = N^2\xi/(pi^2k)\)

• .tintern relaxation time due to internal friction

• .tr_p characteristic times \(tr_p=tr_1 p^{-2}+t_{intern}\)

• .beadfriction

• .ftype type of internal friction

• …. use .attr to see all attributes

Notes

The Rouse model describes beads connected by harmonic springs without hydrodynamic interactions and open ends. The coherent intermediate scattering function \(S(q,t)/S(q,0)\) is [1] [2] :

\[\frac{S(q,t)}{S(q,0)} = \frac{1}{N} e^{-q^2D_{cm}t} \sum_{n,m}^N e^{-\frac{1}{6}q^2B(n,m,t)}\]

\(B(n,m,t)\) describes the internal motions characterised by eigenmodes of the equation 4.II.6 in [1] \(\frac{\zeta_p}{\zeta} k \frac{\partial^2 \Phi_{pn}}{\partial^2 n}=-k_p\Phi_{pn}\) where \(\Phi_{pn}\) describes the delocalisation of bead n in mode p.

The boundary conditions select the eigenmodes from the general form \(\Phi_{pn} = A sin(kn) + Bcos(kn)\)

• Two free ends \(\partial\Phi_{pn}/\partial n=0 \text{ for n=0 and n=N}\) select A=0 and k=pπ/N (equ. 4.II.7+9 in [1]):

  \[B(n,m,t)=|n-m|^{2\mu}l^2 + \sum_{p=1}^{N-1} A_p cos(\pi pn/N)cos(\pi pm/N) (1-e^{-t/t_{zp}})\]

• One fixed and one free end \(\partial\Phi_{pn}/\partial n=0 \text{ at n=0 and } \Phi_{pn}=0\) at N select B=0 and k=(p-1/2)π/N (see [3]):

  \[B(n,m,t)=|n-m|^{2\mu}l^2 + \sum_{p=1-1/2}^{N-1-1/2} A_p sin(\pi pn/N) sin(\pi pm/N) (1-e^{-t/t_{zp}})\]

  With the ends interchanged this can be written like [4] (same result)

  \[B(n,m,t)=|n-m|^{2\mu}l^2 + \sum_{p=1-1/2}^{N-1-1/2} A_p cos(\pi pn/N) cos(\pi pm/N) (1-e^{-t/t_{zp}})\]

• Two fixed ends \(\Phi_{pn}=0\) at n=0 and n=N select B=0 and k=pπ/N:

  \[B(n,m,t)=|n-m|^{2\mu}l^2 + \sum_{p=1}^{N-1} A_p sin(\pi pn/N)sin(\pi pm/N) (1-e^{-t/t_{zp}})\]

For fixed ends the center of mass diffusion Dcm is that of the object where the chain is fixed. The chain dimension is defined by \(R_e=lN^{ .5}\).

Unfortunately there are some papers that give wrong equations for fixed ends Zimmm or Rouse dynamics. The correct equations above can be retrieved from [1] appendix 4.II as solution of the differential equation 4.II.6 above which describes standing waves in a string or in a open tube. The classical Zimm/Rouse describe two open ends.

For detailed description of parameters see finiteRouse().

References

[1] (1,2,3,4)

Doi Edwards Theory of Polymer dynamics in the appendix the equation is found

[2]

Nonflexible Coils in Solution: A Neutron Spin-Echo Investigation of Alkyl-Substituted Polynorbonenes in Tetrahydrofuran Michael Monkenbusch et al.Macromolecules 2006, 39, 9473-9479 The exponential is missing a “t” http://dx.doi.org/10.1021/ma0618979

[3]

Normal Modes of Stretched Polymer Chains Y. Marciano and F. Brochard-Wyart Macromolecules 1995, 28, 985-990 https://doi.org/10.1021/ma00108a028

[4] (1,2)

Polymer Chain Conformation and Dynamical Confinement in a Model One-Component Nanocomposite C. Mark, O. Holderer, J. Allgaier, E. Hübner, W. Pyckhout-Hintzen, M. Zamponi, A. Radulescu, A. Feoktystov, M. Monkenbusch, N. Jalarvo, and D. Richter Phys. Rev. Lett. 119, 047801 (2017), https://doi.org/10.1103/PhysRevLett.119.047801

about internal friction

[7] (1,2)

Internal friction in an intrinsically disordered protein - Comparing Rouse-like models with experiments A. Soranno, F. Zosel, H. Hofmann J. Chem. Phys. 148, 123326 (2018) http://aip.scitation.org/doi/10.1063/1.5009286

Examples

Let us assume we have a core-shell particle with grafted chains on a core (See e.g. Mark et al. [4] for silica nanoparticles with grafted chains) For low aggregation number the chains dont interact and the motions are that of a Rouse chain with one fixed end. The center of mass diffusion is that of the core-shell particle and much slower than \(D_{Rouse}\) but could be determined by PFG-NMR.

For comparison we think of both ends grafted that will make a loop that both ends are fixed (but not at the same position). We neglect any influence of the core onto the chain configuration (at least its only a half space).

We allow a Dcm ≈50 times slower than DRouse.

We observe two relaxations, a faster of the internal dynamics and a slower because of diffusion.

First compare one fixed end (full lines) with the free Rouse (broken lines). For long times the diffusion gets equal visible at low q for long times.

Obviously the amplitude of mode relaxations is much stronger than for open ends due to the different eigenmodes.

import jscatter as js
import numpy as np
t = js.loglist(0.1, 1000, 40)
q=np.r_[0.1:2:0.25]
l=0.38  # nm , bond length amino acids

p=js.grace(1.5,1.5)
p.xaxis(label='q / ns',scale='log')
p.yaxis(label='I(q,t)/I(q,0)')
p.title('Compare 1 fixed to free ends')
p.subtitle('solid line = one fixed end; broken lines = open ends')

# free ends just for comapring
fFR0 = js.dynamic.fixedFiniteRouse(t, q, 124, 40, l=l, Dcm=0.004,frict=9e-14,fixedends=0)
# one fixed end
fFR1 = js.dynamic.fixedFiniteRouse(t, q, 124, 40, l=l, Dcm=0.004,frict=9e-14,fixedends=1)

for i, z in enumerate(fFR1, 1):
    p.plot(z.X, z.Y, line=[1, 3, i], symbol=0, legend=f'q={z.q:.1f} nm\\S-1')
for i, z in enumerate(fFR0, 1):
    p.plot(z.X, z.Y, line=[3, 3, i], symbol=0, legend='')

p.legend(x=0.2,y=0.4,charsize=0.6)

# p.save(js.examples.imagepath+'/fixed_vs_freeRouse.jpg',size=(1.1,1.1))

Now we compare one and two open ends. The differences are marginally and will be difficult to discriminate in real measurements.

import jscatter as js
import numpy as np
t = js.loglist(0.1, 1000, 40)
q=np.r_[0.1:2:0.25]
l=0.38  # nm , bond length amino acids

p=js.grace(1.5,1.5)
p.xaxis(label='q / ns',scale='log')
p.yaxis(label='I(q,t)/I(q,0)')
p.title('Compare 1 fixed to 2 fixed ends')
p.subtitle('solid line = one fixed end; broken lines = 2 fixed ends')

# two fixed ends
fFR2 = js.dynamic.fixedFiniteRouse(t, q, 124, 40, l=l, Dcm=0.004, frict=9e-14, fixedends=2)
# one fixed end
fFR1 = js.dynamic.fixedFiniteRouse(t, q, 124, 40, l=l, Dcm=0.004, frict=9e-14, fixedends=1)

for i, z in enumerate(fFR1, 1):
    p.plot(z.X, z.Y, line=[1, 3, i], symbol=0, legend=f'q={z.q:.1f} nm\\S-1')
for i, z in enumerate(fFR2, 1):
    p.plot(z.X, z.Y, line=[3, 3, i], symbol=0, legend='')

p.legend(x=0.2,y=0.4,charsize=0.6)

# p.save(js.examples.imagepath+'/fixedRouse_1vs2.jpg',size=(1,1))

jscatter.dynamic.timedomain.fixedFiniteZimm(t, q, NN=None, pmax=None, l=None, Dcm=None, Dcmfkt=None, tintern=0.0, mu=0.5, viscosity=1.0, ftype=None, rk=None, Temp=293, fixedends=1)

Zimm dynamics of a chain with fixed ends with internal friction and hydrodynamic interactions.

Opposite to the finiteZimm() here one or both ends are fixed. This might be a chain tethered to a particle that defines the diffusion. Chains are non interacting.

Parameters:

fixedends0,1,2, default = 1

Number of fixed ends. 0 is only for comparison and corresponds to finiteZimm() .

tarray

Time in units nanoseconds.

q: float, array

Scattering vector in units nm^-1. If q is list a dataList is returned otherwise a dataArray is returned.

NNinteger

Number of chain beads.

lfloat, default 1

Bond length between beads; units nm.

pmaxinteger, list of float, default is NN

• integer => maximum mode number taken into account.

• list => list of amplitudes \(a_p > 0\) for individual modes to allow weighing. Not given modes have weight zero.

Dcmfloat

Center of mass diffusion in nm²/ns.

Dcmfktarray 2xN, function

Function f(q) or array with [qi, f(qi)] as correction for Dcm like Diff = Dcm*f(q). e.g. for inclusion of structure factor and hydrodynamic function with f(q)=H(Q)/S(q). Missing values are interpolated. Only array input can be pickled to speedup by using formel.memoize .

tinternfloat>0

Additional relaxation time due to internal friction between neighbouring beads in units ns.

mufloat in range [0.01,0.99]

\(\mu\) describes solvent quality.

• <0.5 collapsed chain

• =0.5 theta solvent 0.5 (gaussian chain)

• =0.6 good solvent

• >0.6 swollen chain

viscosityfloat

\(\eta\) in units cPoise=mPa*s e.g. water \(visc(T=293 K) =1 mPas\)

Tempfloat, default 273+20

Temperature in Kelvin.

type‘czif’, default = ‘zif’

Type of internal friction and interaction modification.

• Default Zimm is used with \(t_{intern}=0\)

• ‘zif’ Internal friction between neighboring beads in chain [3]_.

  \(t_{zp}=t_z p^{-3\mu}+t_{intern}\)

• ‘czif’ Bead confining harmonic potential with internal friction, only for \(\mu=0.5\) [6]_ .

  The beads are confined in an additional harmonic potential with \(\frac{1}{2}k_c(r_n-0)^2\) leading to a more compact configuration. \(rk= k_c/k\) describes the relative strength compared to the force between beads \(k\).

rkNone , float

\(rk= k_c/k\) describes the relative force constant for ftype ‘czif’.

Returns:

dataArrayfor single q

dataListfor multiple q

• [time; Sqt; Sqt_inf; Sqtinc; Sqtz]

• time units ns

• Sqt is coherent scattering with diffusion and mode contributions

• Sqt_inf is coherent scattering with ONLY diffusion (no internal modes)

• Sqtinc is incoherent scattering with diffusion and mode contributions (no separate diffusion)

• Sqt0 is coherent scattering with diffusion and mode contributions, but no Dcmfkt => f(q)=1

• .q wavevector

• .modecontribution \(a_p\) of coherent modes i in sequence as in PRL 71, 4158 equ (3)

• .Re is \(R_e=lN^{\mu}\)

• .tzimm => Zimm time or rotational correlation time

• .t_p characteristic times

• …. use .attr for all attributes

Notes

The Zimm model describes beads connected by harmonic springs with hydrodynamic interaction (see 4.2 in [1]). We find

\[\frac{S(q,t)}{S(q,0)} = \frac{1}{N} e^{-q^2D_{cm}t}\sum_{n,m}^N e^{-\frac{1}{6}q^2B(n,m,t)}\]

\(B(n,m,t)\) describes the internal motions characterised by eigenmodes of the equation 4.II.6 in [1] \(\frac{\zeta_p}{\zeta} k \frac{\partial^2 \Phi_{pn}}{\partial^2 n}=-k_p\Phi_{pn}\) where \(\Phi_{pn}\) describes the delocalisation of bead n in mode p.

The boundary conditions select the eigenmodes from the general form \(\Phi_{pn} = A sin(kn) + Bcos(kn)\)

• Two free ends \(\partial\Phi_{pn}/\partial n=0 \text{ for n=0 and n=N}\) select A=0 and k=pπ/N (equ. 4.II.7+9 in [1]):

  \[B(n,m,t)=|n-m|^{2\mu}l^2 + \sum_{p=1}^{N-1} A_p cos(\pi pn/N)cos(\pi pm/N) (1-e^{-t/t_{zp}})\]

• One fixed and one free end \(\partial\Phi_{pn}/\partial n=0 \text{ at n=0 and } \Phi_{pn}=0\) at N select B=0 and k=(p-1/2)π/N (see [2]):

  \[B(n,m,t)=|n-m|^{2\mu}l^2 + \sum_{p=1-1/2}^{N-1-1/2} A_p sin(\pi pn/N) sin(\pi pm/N) (1-e^{-t/t_{zp}})\]

• Two fixed ends \(\Phi_{pn}=0\) at n=0 and n=N select B=0 and k=pπ/N:

  \[B(n,m,t)=|n-m|^{2\mu}l^2 + \sum_{p=1}^{N-1} A_p sin(\pi pn/N)sin(\pi pm/N) (1-e^{-t/t_{zp}})\]

For fixed ends the center of mass diffusion Dcm is that of the object where the chain is fixed. The chain dimension is defined by \(R_e=lN^{\mu}\).

Unfortunately there are some papers that give wrong equations for fixed end Zimm or Rouse dynamics. The correct equations above can be retrieved from [1] appendix 4.II as solution of the differential equation 4.II.6 above which describes standing waves in a string or in a open tube. The classical Zimm/Rouse describe two open ends.

For detailed description of parameters see finiteZimm().

References

[1] (1,2,3,4)

The Theory of Polymer dynamics Doi, M., & Edwards, S. F. (1988). Clarendon Press.

[2]

Normal Modes of Stretched Polymer Chains Y. Marciano and F. Brochard-Wyart Macromolecules 1995, 28, 985-990 https://doi.org/10.1021/ma00108a028

Examples

Let us assume we have a core shell micelle of diblock copolymers with a hydrophobic part that assemble in the core and the hydrophilic part extended into the solvent. The core is solvent matched and invisible. For low aggregation number the hydrophobic tails extending into the solvent dont interact and the motions are that of a Zimm chain with one fixed end. The center of mass diffusion is that of the micelle and much slower than \(D_{Zimm}\) but could be determined by DLS dilution series or PFG-NMR. (See e.g. Mark et al. https://doi.org/10.1103/PhysRevLett.119.047801 for silica nanoparticles with grafted chains)

For comparison we think of a triblock with hydrophobic ends that will make a loop that both ends are fixed (but not at the same position). The hydrophilic is of same size. We neglect any influence of the core onto the chain configuration.

We allow a Dcm ≈50 times slower than DZimm of the hydrophilic tail.

We observe two relaxations, a faster of the internal dynamics and a slower because of diffusion.

First compare one fixed end (full lines) with the free Zimm (broken lines). For long times the diffusion gets equal visible at low q for long times.

Obviously the amplitude of mode relaxations is much stronger than for open ends due to the different eigenmodes.

import jscatter as js
import numpy as np
t = js.loglist(0.1, 1000, 40)
q=np.r_[0.1:2:0.25]
l=0.38  # nm , bond length amino acids

p=js.grace(1.5,1.5)
p.xaxis(label='q / ns',scale='log')
p.yaxis(label='I(q,t)/I(q,0)')
p.title('Compare 1 fixed to free ends')
p.subtitle('solid line = one fixed end; broken lines = open ends')

# free ends just for comapring
fFZ0 = js.dynamic.fixedFiniteZimm(t, q, 124, 40, l=l, mu=0.5, Dcm=0.004,fixedends=0)
# one fixed end
fFZ1 = js.dynamic.fixedFiniteZimm(t, q, 124, 40, l=l, mu=0.5, Dcm=0.004,fixedends=1)

for i, z in enumerate(fFZ1, 1):
    p.plot(z.X, z.Y, line=[1, 3, i], symbol=0, legend=f'q={z.q:.1f} nm\\S-1')
for i, z in enumerate(fFZ0, 1):
    p.plot(z.X, z.Y, line=[3, 3, i], symbol=0, legend='')

p.legend(x=0.2,y=0.4,charsize=0.6)

# p.save(js.examples.imagepath+'/fixedZimm_vs_freeZimm.jpg',size=(1.,1.))

Now we compare one and two open ends. The differences are marginally and will be difficult to discriminate in real measurements.

import jscatter as js
import numpy as np
t = js.loglist(0.1, 1000, 40)
q=np.r_[0.1:2:0.25]
l=0.38  # nm , bond length amino acids

p=js.grace(1.5,1.5)
p.xaxis(label='q / ns',scale='log')
p.yaxis(label='I(q,t)/I(q,0)')
p.title('Compare 1 fixed to 2 fixed ends')
p.subtitle('solid line = one fixed end; broken lines = 2 fixed ends')

# two fixed ends
fFZ2 = js.dynamic.fixedFiniteZimm(t, q, 124, 40, l=l, mu=0.5, Dcm=0.004, fixedends=2)
# one fixed end
fFZ1 = js.dynamic.fixedFiniteZimm(t, q, 124, 40, l=l, mu=0.5, Dcm=0.004, fixedends=1)

for i, z in enumerate(fFZ1, 1):
    p.plot(z.X, z.Y, line=[1, 3, i], symbol=0, legend=f'q={z.q:.1f} nm\\S-1')
for i, z in enumerate(fFZ2, 1):
    p.plot(z.X, z.Y, line=[3, 3, i], symbol=0, legend='')

p.legend(x=0.2,y=0.4,charsize=0.6)

# p.save(js.examples.imagepath+'/fixedZimm_1vs2_fixed.jpg',size=(1,1))

jscatter.dynamic.timedomain.integralZimm(t, q, Temp=293, viscosity=0.001, amp=1, rtol=0.02, tol=0.02, limit=50)

Conformational dynamics of an ideal chain with hydrodynamic interaction, coherent scattering.

Integral version Zimm dynamics.

Parameters:

tarray

Time points in ns

qfloat

Wavevector in 1/nm

Tempfloat

Temperature in K

viscosityfloat

Viscosity in cP=mPa*s

ampfloat

Amplitude

rtol,tolfloat

Relative and absolute tolerance in scipy.integrate.quad

limitint

Limit in scipy.integrate.quad.

Returns:

dataArray

Notes

The Zimm model describes the conformational dynamics of an ideal chain with hydrodynamic interaction between beads. We use equ 85 and 86 from [1] as

\[S(Q,t) = \frac{12}{Q^2l^2} \int_0^{\infty} e^{-u-(\Omega_Z t)^{2/3} g(u(\Omega_Z t)^{2/3})} du\]

with

\[g(y) = \frac{2}{\pi} \int_0^{\infty} x^{-2}cos(xy)(1-e^{-2^{-0.5}x^{2/3}}) dx\]

\[\Omega_z = \frac{kTQ^3}{6\pi\eta_s}\]

See [1] for details.

References

[1] (1,2)

Neutron Spin Echo Investigations on the Segmental Dynamics of Polymers in Melts, Networks and Solutions in Neutron Spin Echo Spectroscopy Viscoelasticity Rheology Volume 134 of the series Advances in Polymer Science pp 1-129 DOI 10.1007/3-540-68449-2_1

Examples

import jscatter as js
import numpy as np
t=np.r_[0:10:0.2]
p=js.grace()
for q in np.r_[0.26,0.40,0.53,0.79,1.06]:
   iqt=js.dynamic.integralZimm(t=t,q=q,viscosity=0.2e-3)
   p.plot((iqt.X*iqt.q**3)**(2/3.),iqt.Y)
p.xaxis(label=r'(Q\S3\Nt)\S2/3')
p.yaxis(label=r'I(Q,t)/I(Q,0)')
p.title('integral Zimm rescaled by characteristic time')
# p.save(js.examples.imagepath+'/integralZimm.jpg')

jscatter.dynamic.timedomain.jumpDiffusion(t, Q, t0, l0)

Incoherent intermediate scattering function of translational jump diffusion in the time domain.

Parameters:

tarray

Times, units ns

Qfloat

Wavevector, units nm

t0float

Residence time, units ns

l0float

Mean square jump length, units nm

Returns:

dataArray

Notes

We use equ. 3-5 from [1] for random jump diffusion as

\[T(Q,t) = exp(-\Gamma(Q)t)\]

with residence time \(\tau_0\) and mean jump length \(<l^2>^{1/2}_{av}\) and diffusion constant \(D\) in

\[\Gamma(Q) = \frac{DQ^2}{1+DQ^2\tau_0}\]

\[D=\frac{ <l^2>_{av}}{6\tau_0}\]

References

[1]

Experimental determination of the nature of diffusive motions of water molecules at low temperatures J. Teixeira, M.-C. Bellissent-Funel, S. H. Chen, and A. J. Dianoux Phys. Rev. A 31, 1913 – Published 1 March 1985

jscatter.dynamic.timedomain.methylRotation(t, q, t0=0.001, fraction=1, rhh=0.12, beta=0.8)

Incoherent intermediate scattering function of CH3 methyl rotation in the time domain.

Parameters:

tarray

List of times, units ns

qfloat

Wavevector, units nm

t0float, default 0.001

Residence time, units ns

fractionfloat, default 1

Fraction of protons contributing.

rhhfloat, default=0.12

Mean square jump length, units nm

betafloat, default 0.8

exponent

Returns:

dataArray

Notes

According to [1]:

\[I(q,t) = (EISF + (1-EISF) e^{-(\frac{t}{t_0})^{\beta}} )\]

\[EISF=\frac{1}{3}+\frac{2}{3}\frac{sin(qr_{HH})}{qr_{HH}}\]

with \(t_0\) residence time, \(r_{HH}\) proton jump distance.

References

[1]

13. Bée, Quasielastic Neutron Scattering (Adam Hilger, 1988).

[2]

Monkenbusch et al. J. Chem. Phys. 143, 075101 (2015)

Examples

import jscatter as js
import numpy as np
# make a plot of the spectrum
w=np.r_[-100:100]
ql=np.r_[1:15:1]
iqwCH3=js.dL([js.dynamic.time2frequencyFF(js.dynamic.methylRotation,'elastic',w=np.r_[-100:100:0.1],q=q )
                                            for q in ql])
p=js.grace()
p.plot(iqwCH3,le='CH3')
p.yaxis(min=1e-5,max=10,scale='l')

jscatter.dynamic.timedomain.resolution(t, s0=1, m0=0, s1=None, m1=None, s2=None, m2=None, s3=None, m3=None, s4=None, m4=None, s5=None, m5=None, s6=None, m6=None, s7=None, m7=None, a0=1, a1=1, a2=1, a3=1, a4=1, a5=1, a6=1, a7=1, bgr=0, resolution=None)

Resolution in time domain as multiple Gaussians for inelastic measurement as back scattering or time of flight instrument.

Multiple Gaussians define the function to describe a resolution measurement. Use `resolution_w` to fit with the appropriate normalized Gaussians and this function to implicit Fourier transform a signal. See Notes.

Parameters:

tarray

Times

s0,s1,…float

Width of Gaussian functions representing a resolution measurement. The number of si not None determines the number of Gaussians.

m0, m1,….float, None

Means of the Gaussian functions representing a resolution measurement.

a0, a1,….float, None

Amplitudes of the Gaussian functions representing a resolution measurement.

bgrfloat, default=0

Background

resolutiondataArray

Resolution with attributes sigmas, amps which are used instead of si, ai.

• If resolution is from w domain this represents the Fourier transform from w to t domain. means are NOT used from w domain as these result only in a phase shift, instead m0..m5 are used. If mi is not give zero is assumed.

• If from t domain the resolution is recalculated with same parameters for new t.

Returns:

dataArray

Notes

In a typical inelastic experiment the resolution is measured by e.g. a vanadium measurement (elastic scatterer). In t domain (Neutron Spin Echo) this is a carbon black sample for small Q or e.g. Zirconium for higher Q. In w domain the resolution is described by a multi Gaussian function as in resw=resolution_w(w,…) with amplitudes \(ai_w\), width \(si_w\) and common mean \(m_w\).

resolution(t,resolution_w=resw) defines the Fourier transform of resolution_w using the same coefficients as an implicit Fourier transform. \(mi_t\) are set by default to zero as \(mi_w\) lead only to a phase shift. It is easiest to shift w values in w domain as it corresponds to a shift of the elastic line.

Beside the fitting of resolution measurements the pair of resolution_w and resolution allows a Fourier transform from w to t domain of any signal. If resolution_w is used for fitting of data in the w domain then `ft = resolution(t=..,resolution=resolution_w_fit)` represents the Fourier transform of the fitted data.

The used Gaussians are normalized that they are a pair of Fourier transforms:

\[R_t(t,m_i,s_i,a_i)=\sum_i a_i s_i e^{-\frac{1}{2}s_i^2 t^2} \Leftrightarrow R_w(w,m_i,s_i,a_i)= \sum_i a_i e^{-\frac{1}{2}(\frac{w-m_i}{s_i})^2}\]

under the Fourier transform defined as

\[F(f(t)) = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{\infty} f(t) e^{-i\omega t} dt\]

\[F(f(w)) = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{\infty} f(\omega) e^{i\omega t} d\omega\]

Examples

Using the result of a fit in w domain to represent the resolution in time domain :

import jscatter as js
import numpy as np

# resw is a resolution in w domain maybe as a result from a fit to vanadium data
# resw contains all parameters
w = np.r_[-100:100:0.5]
resw = js.dynamic.resolution_w(w, s0=12, m0=0, a0=2)

# representing the Fourier transform of resw as a gaussian transforms to time domain
t = np.r_[0:1:0.01]
rest = js.dynamic.resolution(t,resolution=resw)
t2 = np.r_[0:0.5:0.005]
rest2 = js.dynamic.resolution(t2,resolution=rest)

jscatter.dynamic.timedomain.simpleDiffusion(t, gamma=None, q=None, D=None, w=0, beta=1, type='lognorm')

Intermediate scattering function [g1(t)] for diffusing particles from distribution of relaxation rates.

\[I(q,t,D, \sigma ) = \beta \int g(\Gamma, \Gamma_0, \sigma ) e^{-\Gamma t}\]

and relaxation rate \(\Gamma_0=q^2D\).

Parameters:

tfloat, array

Times

gammafloat

Mean relaxation rate in inverse t units. Overrides q and D if given. If q and D given gamma=q*q*D

qfloat, array

Wavevector

betafloat

Intercept \(\beta\) in DLS. The amplitude prefactor.

Dfloat

Mean diffusion coefficient.

wfloat

Relative standard deviation of the diffusion coefficient distribution. In absolute units \(\sigma=w*q^2*D\). For a typical DLS experiment w≈0.25 just from instrument noise (e.g. noise ≈ 1e-3 Zetasizer Nano, Malvern)

type‘truncnorm’, default ‘lognorm’

Distribution shape.

• ‘lognorm’ lognorm distribution as normal distribution on a log scale.

  \[g(x, \mu, \sigma) = \frac{ 1 }{\ x\sigma\sqrt{2\pi}} exp(-\frac{\ln(x- \mu)^2}{ 2 \sigma^2 })\]

• ‘truncnorm’ normal distribution cut at zero.

\[g(x, \mu, \sigma)= e^{-0.5(\frac{x-\mu}{\sigma})^2} / (\sigma\sqrt{2\pi}) \ \text{ for x>0}\]

Returns:

outdataArray

intermediate scattering function or \(g_1\)

• .D, .wavevector, .beta respective input parameters

• pdf : Probability of the distribution in the interval around pdf[0,i] (half distance to neighboring points) that sum(pdf[2])==1 similar to CONTIN results.

Notes

Units of q, t and D result in unit-less [q*q*D*t] like q in 1/cm, t in s -> D in cm*cm/s .

Examples

import jscatter as js
import numpy as np

t = js.loglist(1e-6,10,1000) # in seconds

# ≈ a protein with a MW of 140kDa
D = 3e-7  # unit cm^2/s
q = 4*np.pi/633e-7*np.sin(np.pi/4)  # 90º HeNe laser in DLS

p=js.grace(1.8,1)
p.multi(1,2)
p[0].xaxis(label=r't / s ',scale='log')
p[0].yaxis(label=r'g\s1\N(t) ')
p[1].xaxis(label=r'\xG\f{} / 1/s ',scale='log')
p[1].yaxis(label=[r'P(\xG\f{})',1,'opposite'],)

for c,w in enumerate([0.25,0.5,1,2],1):
   dls = js.dynamic.simpleDiffusion(t=t,q=q,D=D,w=w)
   p[0].plot(dls,sy=0,li=[1,3,c],le=f'w={w}')
   p[1].plot(dls.pdf[0], 20 * dls.pdf[1],sy=0,li=[1,3,c])

p[0].legend(x=0.01,y=0.8)
p[0].title('DLS correlation')
p[1].title('rate distribution')
# p.save(js.examples.imagepath+'/simpleDiffusion.jpg',size=(1.8,1))

jscatter.dynamic.timedomain.stretchedExp(t, gamma, beta, amp=1)

Stretched exponential function.

\[I(t) = amp\, e^{-(t\gamma)^\beta}\]

Parameters:

tarray

Times

gammafloat

Relaxation rate in units 1/[unit t]

betafloat

Stretched exponent

ampfloat default 1

Amplitude

Returns:

dataArray

jscatter.dynamic.timedomain.transRotDiffusion(t, q, cloud, Dr, Dt=0, lmax='auto')

Translational + rotational diffusion of an object (dummy atoms); dynamic structure factor in time domain.

A cloud of dummy atoms can be used for coarse graining of a non-spherical object e.g. for amino acids in proteins. On the other hand its just a way to integrate over an object e.g. a sphere or ellipsoid (see example). We use [2] for an objekt of arbitrary shape modified for incoherent scattering.

Parameters:

tarray

Times in ns.

qfloat

Wavevector in units 1/nm

cloudarray Nx3, Nx4 or Nx5 or float

• A cloud of N dummy atoms with positions cloud[:3] in units nm that describe an object .

• If given, cloud[3] is the incoherent scattering length \(b_{inc}\) otherwise its equal 1.

• If given, cloud[4] is the coherent scattering length \(b_{coh}\) otherwise its equal 1.

• If cloud is single float the value is used as radius of a sphere with 10x10x10 grid points.

Drfloat

Rotational diffusion constant (scalar) in units 1/ns.

Dtfloat, default=0

Translational diffusion constant (scalar) in units nm²/ns.

lmaxint

Maximum order of spherical bessel function. ‘auto’ -> lmax > 2π r.max()*q/6.

Returns:

dataArray

Columns [t; Iqtinc; Iqtcoh; Iqttrans]

• .radiusOfGyration

• .Iq_coh coherent scattering (formfactor)

• .Iq_inc incoherent scattering

• .wavevector

• .rotDiffusion

• .transDiffusion

• .lmax

Notes

We calculate the field autocorrelation function given in equ 24 in [2] for an arbitrary rigid object without additional internal dynamic as

\[I(q,t) = e^{-q^2D_tt} I_{rot}(q,t) = e^{-q^2D_tt} \sum_l S_{l,i/c}(q)e^{-l(l+1)D_rt}\]

where \(I_{rot}(q,t)\) is the rotational diffusion contribution and

\[ \begin{align}\begin{aligned}\begin{split}S_{l,c}(q) &= 4\pi \sum_m |\sum_i b_{i,coh} j_l(qr_i) Y_{l,m}(\Omega_i)|^2 & coherent scattering \\\end{split}\\\begin{split}S_{l,i}(q) &= \sum_m \sum_i (2l+1) b_{i,inc}^2 |j_l(qr_i)|^2 & incoherent scattering\\\end{split}\end{aligned}\end{align} \]

and coh/inc scattering length \(b_{i,coh/inc}\), position vector \(r_i\) and orientation of atoms \(\Omega_i\), spherical Bessel function \(j_l(x)\), spherical harmonics \(Y_{l,m}(\Omega_i)\).

• The incoherent intermediate scattering function is res.Y/res.Iq_inc or res._Iqtinc/res.Iq_inc

• The coherent intermediate scattering function is res._Iqtcoh/res.Iq_coh

• For real scattering data as backscattering or spinecho coherent and incoherent have to be mixed according to the polarisation conditions of the experiment accounting also for spin flip probability of coherent and incoherent scattering. For the simple case of non-polarised measurement we get

\[I(q,t)/I(q,0) = \frac{I_{coh}(q,t)+I_{inc}(q,t)}{I_{coh}(q,0)+I_{inc}(q,0)}\]

References

[1]

Incoherent scattering law for neutron quasi-elastic scattering in liquid crystals. Dianoux, A., Volino, F. & Hervet, H. Mol. Phys. 30, 37–41 (1975).

[2] (1,2)

Effect of rotational diffusion on quasielastic light scattering from fractal colloid aggregates. Lindsay, H., Klein, R., Weitz, D., Lin, M. & Meakin, P. Phys. Rev. A 38, 2614–2626 (1988).

Examples

A bit artificial look at only rotational diffusion of a superball build from dummy atoms. (rotational diffusion should only show if also translational diffusion is seen) Change p to change from spherical shape (p=1) to cube (p>10) or star like (p<0.5) (use grid.show() to take a look at the shape) The coherent contribution is suppressed for low q if the particle is spherical .

import jscatter as js
import numpy as np
R=2;NN=10
ql=np.r_[0.4:2.:0.3,2.1:15:2]
t=js.loglist(0.001,50,50)
# get superball
p2=1
grid=js.ff.superball(ql,R,p=p2,nGrid=NN,returngrid=True)
Drot=js.formel.Drot(R)
Dtrans=js.formel.Dtrans(R)
p=js.grace(1.5,1)
p.new_graph(xmin=0.23,xmax=0.43,ymin=0.25,ymax=0.55)
iqt=js.dL([js.dynamic.transRotDiffusion(t,q,grid.XYZ,Drot,lmax=30) for q in ql])

for i,iiqt in enumerate(iqt,1):
    p[0].plot(iiqt.X,iiqt.Y/iiqt.Iq_inc,li=[1,3,i],sy=0,le=f'q={iiqt.wavevector:.1f} nm\S-1')
    p[0].plot(iiqt.X,iiqt._Iqtcoh/iiqt.Iq_coh,li=[3,3,i],sy=0,le=f'q={iiqt.wavevector:.1f} nm\S-1')

p[1].plot(iqt.wavevector,iqt.Iq_coh.array/grid.numberOfAtoms(),li=1)
p[1].plot(iqt.wavevector,iqt.Iq_inc.array/grid.numberOfAtoms(),li=1)
p[0].xaxis(scale='l',label='t / ns',max=200,min=0.001)
p[0].yaxis(scale='n',label='I(q,t)/I(q,0)')
p[1].xaxis(scale='n',label='q / nm\S-1')
p[1].yaxis(scale='l',label='I(q,t=0)')

p[0].legend(x=60,y=1.1,charsize=0.7)
p[0].title(f'rotational diffusion of superball with p={p2:.2f}')
p[0].subtitle(f'coh relevant only at high q for sphere')
p[1].subtitle('coh + inc scattering')
p[0].text(x=0.0015,y=0.8,string=r'lines inc\ndashed coh',charsize=1.5)
#p.save(js.examples.imagepath+'/rotDiffusion.jpg')

# Second example
# non-polarized experiment
p=js.grace(1.5,1)
grid=js.ff.superball(ql,R,p=1.,nGrid=10,returngrid=True)
iqt=js.dL([js.dynamic.transRotDiffusion(t,q,grid.XYZ,Drot,Dtrans,lmax=30) for q in ql])
for i,iiqt in enumerate(iqt,1):
    p.plot(iiqt.X,(iiqt._Iqtinc+iiqt._Iqtcoh)/(iiqt.Iq_inc+iiqt.Iq_coh),li=[1,3,i],sy=0,le=f'q={iiqt.wavevector:.1f} nm\S-1')
    p.plot(iiqt.X,iiqt._Iqtcoh/iiqt.Iq_coh,li=[3,3,i],sy=0,le=f'q={iiqt.wavevector:.1f} nm\S-1')

p.xaxis(scale='l',label='t / ns',max=200,min=0.001)
p.yaxis(scale='n',label='I(q,t)/I(q,0)')
p[0].legend(x=60,y=1.1,charsize=0.7)
p[0].title(f'translational/rotational diffusion of superball with p={p2:.2f}')
p[0].text(x=0.0015,y=0.5,string=r'lines coh+inc\ndashed only coh',charsize=1.5)
#p.save(js.examples.imagepath+'/transrotDiffusion.jpg')

jscatter.dynamic.timedomain.zilmanGranekBicontinious(t, q, xi, kappa, eta, mt=1, amp=1, eps=1, nGauss=60)

Dynamics of bicontinuous micro emulsion phases. Zilman-Granek model as equ B10 in [1]. Coherent scattering.

On very local scales (however larger than the molecular size) Zilman and Granek represent the amphiphile layer in the bicontinuous network as consisting of an ensemble of independent patches at random orientation of size equal to the correlation length xi. Uses Gauss integration and multiprocessing.

Parameters:

tarray

Time values in ns

qfloat

Scattering vector in 1/A

xifloat

Correlation length related to the size of patches which are locally planar and determine the width of the peak in static data. unit A A result of the teubnerStrey model to e.g. SANS data. Determines kmin=eps*pi/xi .

kappafloat

Apparent single membrane bending modulus, unit kT

etafloat

Solvent viscosity, unit kT*A^3/ns=100/(1.38065*T)*eta[unit Pa*s] Water about 0.001 Pa*s = 0.000243 kT*A^3/ns

ampfloat, default = 1

Amplitude scaling factor

epsfloat, default=1

Scaling factor in range [1..1.3] for kmin=eps*pi/xi and rmax=xi/eps. See [1].

mtfloat, default 0.1

Membrane thickness in unit A as approximated from molecular size of material. Determines kmax=pi/mt. About 12 Angstrom for tenside C10E4.

nGaussint, default 60

Number of points in Gauss integration

Returns:

dataList

Notes

See equ B10 in [1] :

\[S(q,t) = \frac{2\pi\xi^2}{a^4} \int_0^1 d\mu \int_0^{r_{max}} dr rJ_0(qr\sqrt{1-\mu^2}) e^{-kT/(2\pi\kappa)q^2\mu^2 \int_{k_{min}}^{k_{max}} dk[1-J_0(kr)e^{w(k)t}]/k^3}\]

with \(\mu = cos(\sphericalangle(q,surface normal))\) , \(J_0\) as Bessel function of order 0

• For technical reasons, in order to avoid numerical difficulties, the real space upper (rmax integration) cutoff was realized by multiplying the integrand with a Gaussian having a width of eps*xi and integrating over [0,3*eps*xi].

References

[1] (1,2,3)

Dynamics of bicontinuous microemulsion phases with and without amphiphilic block-copolymers M. Mihailescu, M. Monkenbusch et al J. Chem. Phys. 115, 9563 (2001); http://dx.doi.org/10.1063/1.1413509

Examples

import jscatter as js
import numpy as np
t=js.loglist(0.1,30,20)
p=js.grace()
iqt=js.dynamic.zilmanGranekBicontinious(t=t,q=np.r_[0.03:0.2:0.04],xi=110,kappa=1.,eta=0.24e-3,nGauss=60)
p.plot(iqt)

# to use the multiprocessing in a fit of data use memoize
data=iqt                          # this represent your measured data
tt=list(set(data.X.flatten))      # a list of all time values
tt.sort()

# use correct values from data for q     -> interpolation is exact for q and tt
zGBmem=js.formel.memoize(q=data.q,t=tt)(js.dynamic.zilmanGranekBicontinious)
def mfitfunc(t, q, xi, kappa, eta, amp):
   # this will calculate in each fit step for for Q (but calc all) and then take from memoized values
   res= zGBmem(t=t, q=q, xi=xi, kappa=kappa, eta=eta, amp=amp)
   return res.interpolate(q=q,X=t)[0]
# use mfitfunc for fitting with multiprocessing

jscatter.dynamic.timedomain.zilmanGranekLamellar(t, q, df, kappa, eta, mu=0.001, eps=1, amp=1, mt=0.1, nGauss=40)

Dynamics of lamellar microemulsion phases. Zilman-Granek model as Equ 16 in [1]. Coherent scattering.

Oriented lamellar phases at the length scale of the inter membrane distance and beyond are performed using small-angle neutrons scattering and neutron spin-echo spectroscopy.

Parameters:

tarray

Time in ns

qfloat

Scattering vector

dffloat

• film-film distance. unit A

• This represents half the periodicity of the structure, generally denoted by d=0.5df which determines the peak position and determines kmin=eps*pi/df

kappafloat

Apparent single membrane bending modulus, unit kT

mufloat, default 0.001

Angle between q and surface normal in unit rad. For lamellar oriented system this is close to zero in NSE.

etafloat

Solvent viscosity, unit kT*A^3/ns = 100/(1.38065*T)*eta[unit Pa*s] Water about 0.001 Pa*s = 0.000243 kT*A^3/ns

epsfloat, default=1

Scaling factor in range [1..1.3] for kmin=eps*pi/xi and rmax=xi/eps

ampfloat, default 1

Amplitude scaling factor

mtfloat, default 0.1

Membrane thickness in unit A as approximated from molecular size of material. Determines kmax=pi/mt About 12 Angstrom for tenside C10E4.

nGaussint, default 40

Number of points in Gauss integration

Returns:

dataList

Notes

See equ 16 in [1] :

\[S(q,t) \propto \int_0^{r_{max}} dr r J_0(q_{\perp}r) exp \Big( -\frac{kT}{2\pi\kappa} q^2\mu^2 \int_{k_{min}}^{k_{max}} \frac{dk}{k^3} [1-J_0(kr) e^{w^\infty(k)t}] \Big)\]

with \(w^{\infty(k) = k^3\kappa/4\overline{\eta}}\), \(\mu = cos(\sphericalangle(q,surface normal))\) ,

\(J_0\) as Bessel function of order 0. For details see [1].

The integrations are done by nGauss point Gauss quadrature, except for the kmax-kmin integration which is done by adaptive Gauss integration with rtol=0.1/nGauss k< kmax/8 and rtol=1./nGauss k> kmax/8.

References

[1] (1,2,3)

Neutron scattering study on the structure and dynamics of oriented lamellar phase microemulsions M. Mihailescu, M. Monkenbusch, J. Allgaier, H. Frielinghaus, D. Richter, B. Jakobs, and T. Sottmann Phys. Rev. E 66, 041504 (2002)

Examples

import jscatter as js
import numpy as np
t=js.loglist(0.1,30,20)
ql=np.r_[0.08:0.261:0.03]
p=js.grace()
iqt=js.dynamic.zilmanGranekLamellar(t=t,q=ql,df=100,kappa=1,eta=2*0.24e-3)
p.plot(iqt)
p.yaxis(label=r'I(Q,t)',min=1e-6,max=1)
p.xaxis(label=r'Q / nm\S-1')
# p.save(js.examples.imagepath+'/zilmanGranekLamellar.jpg', size=(2,2))

jscatter.dynamic.frequencydomain.diffusionHarmonicPotential_w(w, q, tau, rmsd, ndim=3, nmax='auto')

Diffusion in a harmonic potential for dimension 1,2,3 (isotropic averaged), dynamic structure factor in w domain.

An approach worked out by Volino et al.[Rad1dbfb1be11-1]_ assuming Gaussian confinement and leads to a more efficient formulation by replacing the expression for diffusion in a sphere with a simpler expression pertaining to a soft confinement in harmonic potential. Ds = ⟨u**2⟩/t0

Parameters:

warray

Frequencies in 1/ns

qfloat

Wavevector in nm**-1

taufloat

Mean correlation time time. In units ns.

rmsdfloat

Root mean square displacement (width) of the Gaussian in units nm.

ndim1,2,3, default=3

Dimensionality of the potential.

nmaxint,’auto’

Order of expansion. ‘auto’ -> nmax = min(max(int(6*q * q * u2),30),1000)

Returns:

dataArray

Notes

Volino et al.[Rad1dbfb1be11-1]_ compared the behaviour of this approach to the well known expression for diffusion in a sphere. Even if the details differ, the salient features of both models match if the radius R**2 ≃ 5*u0**2 and the diffusion constant inside the sphere relates to the relaxation time of particle correlation t0= ⟨u**2⟩/Ds towards the Gaussian with width u0=⟨u**2⟩**0.5.

\[I_s(Q_x,\omega) = A_0(Q) + \sum_n^{\infty} A_n(Q) L_n(\omega) \; with \; L_n(\omega) = \frac{\tau_0 n}{\pi (n^2+ \omega^2\tau_0^2)}\]

ndim=3

Here we use the Fourier transform of equ 23 with equ. 27a+b in [1]. For order n>30 the Stirling approximation for n! in equ 27b of [1] is used.

\[A_0(Q) = e^{-Q^2\langle u^2_x \rangle}\]

\[A_n(Q,\omega) = e^{-Q^2\langle u^2_x \rangle} \frac{(Q^2\langle u^2_x \rangle)^n}{n!}\]

ndim=2

Here we use the Fourier transform of equ 23 with equ. 28a+b in [1].

\[A_0(Q) = \frac{\sqrt{\pi} e^{-Q^2\langle u^2_x \rangle}}{2} \frac{erfi(\sqrt{Q^2\langle u^2_x \rangle})}{\sqrt{Q^2\langle u^2_x \rangle}}\]

\[A_n(Q,\omega) = \frac{\sqrt{\pi} (Q^2\langle u^2_x \rangle)^n}{2} \frac{F_{1,1}(1+n;3/2+n;-Q^2\langle u^2_x \rangle)}{\Gamma(3/2+n)}\]

with \(F_{1,1}(a,b,z)\) Kummer confluent hypergeometric function, Gamma function \(\Gamma\) and erfi is the imaginary error function erf(iz)/i

ndim=1

The equation given by Volino (29a+b in [1]) seems to be wrong as a comparison with the Fourier transform and the other dimensions shows. Use the model from time domain and use FFT as shown in the example.

For experts: To test this remove a flag in the source code and compare.

References

[1] (1,2,3,4)

Gaussian model for localized translational motion: Application to incoherent neutron scattering. Volino, F., Perrin, J. C. & Lyonnard, S. J. Phys. Chem. B 110, 11217–11223 (2006).

Examples

import jscatter as js
import numpy as np
t2f = js.dynamic.time2frequencyFF
dHP = js.dynamic.diffusionHarmonicPotential
w = np.r_[-100:100]
ql = np.r_[1,3,6,9,12,15]
iqt3 = js.dL([js.dynamic.diffusionHarmonicPotential_w(w=w,q=q,tau=0.14,rmsd=0.34,ndim=3) for q in ql])
iqt2 = js.dL([js.dynamic.diffusionHarmonicPotential_w(w=w,q=q,tau=0.14,rmsd=0.34,ndim=2) for q in ql])
# as ndim=1 is a wrong solution use this instead
# To move spectral leakage out of our window we increase w and interpolate.
# The needed factor (here 23) depends on the quality of your data and background contribution.
# You may test it using ndim=2 in this example.
iqt1 = js.dL([t2f(dHP,'elastic',w=w*23,q=q, rmsd=0.34, tau=0.14 ,ndim=1).interpolate(w) for q in ql])

p=js.grace(1,1)
p.multi(2,3)
p[1].title('diffusionHarmonicPotential for ndim= 1,2,3')
for i,(i3,i2,i1) in enumerate(zip(iqt3,iqt2,iqt1)):
    p[i].plot(i3,li=1,sy=0,le='$wavevector nm\S-1')
    p[i].plot(i2,li=2,sy=0)
    p[i].plot(i1,li=4,sy=0)
    p[i].yaxis(scale='log')
    if i in [1,2,4,5]:p[i].yaxis(ticklabel=0)
    p[i].legend(x=5,y=1, charsize=0.7)
p[0].xaxis(label='')
p[0].yaxis(label=r'S(\xw)')
p[3].yaxis(label=r'S(\xw)')
# p.save(js.examples.imagepath+'/diffusionHarmonicPotential.jpg', size=(2,2))

jscatter.dynamic.frequencydomain.diffusionInSphere_w(w, q, D, R)

Diffusion inside of a sphere; dynamic structure factor in w domain.

Parameters:

warray

Frequencies in 1/ns

qfloat

Wavevector in nm**-1

Dfloat

Diffusion coefficient in units nm**2/ns

Rfloat

Radius of the sphere in units nm.

Returns:

dataArray

Notes

Here we use equ. 33 in [1]

\[S(q,\omega) = A_0^0(q) \delta(\omega) + \frac{1}{\pi} \sum_{l,n\ne 0,0}(2l+1)A_n^l(q) \frac{(x_n^l)^2D/a^2}{[(x_n^l)^2D/a^2]^2 + \omega^2}\]

with \(x_n^l\) as the first 99 solutions of equ 27 a+b as given in [1] and

\[A_0^0(q) = \big[ \frac{3j_1(qa)}{qa} \big]^2 , \; (l,n) = (0,0)\]

\[ \begin{align}\begin{aligned}A_n^l(q) &= \frac{6(x_n^l)^2}{(x_n^l)^2-l(l+1)} \big[\frac{qaj_{l+1}(qa)-lj_l(qa)}{(qa)^2-(x_n^l)^2}\big]^2 \; for \; qa\ne x_n^l\\&= \frac{3}{2}j_l^2(x_n^l) \frac{(x_n^l)^2-l(l+1)}{(x_n^l)^2} \; for \; qa = x_n^l\end{aligned}\end{align} \]

This is valid for qR<20 with accuracy of ~0.001 as given in [1]. If we look at a comparison with free diffusion the valid range seems to be smaller.

A comparison of diffusion in different restricted geometry is show in example A comparison of different dynamic models in frequency domain.

References

[1] (1,2,3)

Neutron incoherent scattering law for diffusion in a potential of spherical symmetry: general formalism and application to diffusion inside a sphere. Volino, F. & Dianoux, A. J., Mol. Phys. 41, 271–279 (1980). https://doi.org/10.1080/00268978000102761

Examples

import jscatter as js
import numpy as np
w=np.r_[-100:100]
ql=np.r_[1:14.1:1.3]
p=js.grace(1,1)
iqw=js.dL([js.dynamic.diffusionInSphere_w(w=w,q=q,D=0.14,R=0.2) for q in ql])
p.plot(iqw)
p.yaxis(label=r'S(\xw)',scale='l')
p.xaxis(label=r'\xw\f{} / ns\S-1')
# p.save(js.examples.imagepath+'/diffusionInSphere_w.jpg', size=(2,2))

jscatter.dynamic.frequencydomain.elastic_w(w)

Elastic line; dynamic structure factor in w domain.

Parameters:

warray

Frequencies in 1/ns

Returns:

dataArray

jscatter.dynamic.frequencydomain.jumpDiff_w(w, q, t0, r0)

Jump diffusion; dynamic structure factor in w domain.

Jump diffusion as a Markovian random walk. Jump length distribution is a Gaussian with width r0 and jump rate distribution with width G (Poisson). Diffusion coefficient D=r0**2/2t0.

Parameters:

warray

Frequencies in 1/ns

qfloat

Wavevector in nm**-1

t0float

Mean residence time in a Poisson distribution of jump times. In units ns. G = 1/tg = Mean jump rate

r0float

Root mean square jump length in 3 dimensions <r**2> = 3*r_0**2

Returns:

dataArray

Notes

Equ 6 + 8 in [1] :

\[ \begin{align}\begin{aligned}S_{inc}(q,\omega) = \frac{1}{\pi} \frac{\Delta\omega}{\Delta\omega^2 + \omega^2}\\with \; \Delta\omega = \frac{1-e^{-q^2 r_0^2/2}}{t_0}\end{aligned}\end{align} \]

References

[1]

Incoherent neutron scattering functions for random jump diffusion in bounded and infinite media. Hall, P. L. & Ross, D. K. Mol. Phys. 42, 637–682 (1981).

jscatter.dynamic.frequencydomain.nSiteJumpDiffusion_w(w, q, N, t0, r0)

Random walk among N equidistant sites (isotropic averaged); dynamic structure factor in w domain.

E.g. for CH3 group rotational jump diffusion over 3 sites.

Parameters:

warray

Frequencies in 1/ns

q: float

Wavevector in units 1/nm

Nint

Number of jump sites, jump angle 2pi/N

r0float

Distance of sites from center of rotation. For CH3 e.g.0.12 nm.

t0float

Rotational correlation time.

Returns:

dataArray

Notes

Equ. 24 [1] :

\[S_{inc}^{rot}(Q,\omega) = B_0(Qa)\delta(\omega) + \frac{1}{\pi} \sum_{n=1}^{N-1} B_n(Qa) \frac{\tau_n}{1+(\omega\tau_n)^2}\]

with \(\tau_1=\frac{\tau}{1-cos(2\pi/N)}\) , \(\tau_n=\tau_1\frac{sin^2(\pi/N)}{sin^2(n\pi/N)}\)

\[B_n(Qa) = \frac{1}{N} \sum_{p=1}^{N} j_0 \Big( 2Qa sin(\frac{\pi p}{N}) \Big) cos(n\frac{2\pi p}{N})\]

References

[1]

Incoherent scattering law for neutron quasi-elastic scattering in liquid crystals. Dianoux, A., Volino, F. & Hervet, H., Mol. Phys. 30, 37–41 (1975). https://doi.org/10.1080/00268977500102721

Examples

import jscatter as js
import numpy as np
w=np.r_[-100:100:0.1]
ql=np.r_[1:14.1:1.3]
p=js.grace()
iqw=js.dL([js.dynamic.nSiteJumpDiffusion_w(w=w,q=q,N=3,t0=0.01,r0=0.12) for q in ql])
p.plot(iqw)
p.yaxis(scale='l',label=r'S(\xw\f{}) / a.u.',min=1e-6,max=1)
p.xaxis(label=r'\xw\f{} / ns\S-1',min=-100,max=100)
# p.save(js.examples.imagepath+'/nSiteJumpDiffusion_w.jpg', size=(2,2))

jscatter.dynamic.frequencydomain.resolution_w(w, s0=1, m0=0, s1=None, m1=None, s2=None, m2=None, s3=None, m3=None, s4=None, m4=None, s5=None, m5=None, s6=None, m6=None, s7=None, m7=None, a0=1, a1=1, a2=1, a3=1, a4=1, a5=1, a6=1, a7=1, bgr=0, resolution=None)

Resolution as multiple Gaussians for inelastic measurement as backscattering or time of flight instrument in w domain.

Multiple Gaussians define the function to describe a resolution measurement. Use only a common mi to account for a shift. See resolution for transform to time domain.

Parameters:

warray

Frequencies

s0,s1,…float

Sigmas of several Gaussian functions representing a resolution measurement. The number of si not none determines the number of Gaussians.

m0, m1,….float, None

Means of the Gaussian functions representing a resolution measurement.

a0, a1,….float, None

Amplitudes of the Gaussian functions representing a resolution measurement.

bgrfloat, default=0

Background

resolutiondataArray

Resolution with attributes sigmas, amps which are used instead of si, ai.

• If from t domain this represents the Fourier transform from w to t domain. The means are NOT used from as these result only in a phase shift, instead m0..m5 are used.

• If from w domain the resolution is recalculated.

Returns:

dataArray

.means .amps .sigmas

Notes

In a typical inelastic experiment the resolution is measured by e.g. a vanadium measurement (elastic scatterer). This is described in w domain by a multi Gaussian function as in resw=resolution_w(w,…) with amplitudes \(a_{iw}\), width sigma \(s_{iw}\) and common mean \(m_w\). To allow asymetric resolutions as observed on some instruments we use mean \(m_{iw}\)

resolution(t,resolution_w=resw) defines the Fourier transform of resolution_w using the same coefficients. \(m_{it}\) are set by default to 0 (if not explicit set) as \(m_{iw}\) lead only to a phase shift. It is easiest to shift w values in w domain as it corresponds to a shift of the elastic line.

The used Gaussians are normalized that they are a pair of Fourier transforms:

\[R_t(t,m_i,s_i,a_i)=\sum_i a_i s_i e^{-\frac{1}{2}s_i^2 t^2} \Leftrightarrow R_w(w,m_i,s_i,a_i)=\sum_i a_i e^{-\frac{1}{2}(\frac{w-m_i}{s_i})^2}\]

under the Fourier transform defined as

\[F(f(t)) = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{\infty} f(t) e^{-i\omega t} dt\]

\[F(f(w)) = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{\infty} f(\omega) e^{i\omega t} d\omega\]

Examples

Transform from and to time domain

import jscatter as js
import numpy as np
# resw is a resolution in w domain maybe as a result from a fit to vanadium data
# resw contains all parameters
w=np.r_[-100:100:0.5]
resw=js.dynamic.resolution_w(w, s0=12, m0=0, a0=2)

w2=np.r_[0:50:0.2]
rest2=js.dynamic.resolution_w(w2,resolution=resw)

# representing the Fourier transform of to time domain
t=np.r_[0:1:0.01]
rest=js.dynamic.resolution(t,resolution=resw)

Sequential fit in w domain to a measurement with realistic data. The data file is from the SPHERE instrument at MLZ Garching (usually not gziped). The file needs to be split to be easily read.

import jscatter as js
import numpy as np
import gzip

with gzip.open(js.examples.datapath +'/Vana.inx.gz','rt') as f:
   lines = f.readlines()
vana = js.dL()
for j in np.r_[0:int(len(lines)//(563))]:
    vana.append(js.dA(lines[j*563:(j+1)*563],lines2parameter=[0,2,3],usecols=[1,2,3]))
    vana[-1].q=float(vana[-1].line_2[0])  # extract q values

start={'s0':0.5,'m0':0,'a0':1,'s1':1,'m1':0,'a1':1,'s2':10,'m2':0,'a2':1,'bgr':0.0073}
dm=5
for van in vana[:1]:
    van.setlimit(m0=[-dm,dm],m1=[-dm,dm],m2=[-dm,dm],m3=[-dm,dm],m4=[-dm,dm],m5=[-dm,dm])
    van.fit(js.dynamic.resolution_w,start,{},{'w':'X'})
    van.showlastErrPlot(yscale='l', fitlinecolor=11)

# vana[7].savelastErrPlot(js.examples.imagepath+'/resolutionfit.jpg')

jscatter.dynamic.frequencydomain.rotDiffusion_w(w, q, cloud, Dr, lmax='auto')

Rotational diffusion of an object (dummy atoms); dynamic structure factor in w domain.

A cloud of dummy atoms can be used for coarse graining of a non-spherical object e.g. for amino acids in proteins. On the other hand its just a way to integrate over an object e.g. a sphere or ellipsoid. We use [2] for an objekt of arbitrary shape modified for incoherent scattering.

Parameters:

warray

Frequencies in 1/ns

qfloat

Wavevector in units 1/nm

cloudarray Nx3, Nx4 or Nx5 or float

• A cloud of N dummy atoms with positions cloud[:3] that describe an object.

• If given, cloud[3] is the incoherent scattering length \(b_{inc}\) otherwise its equal 1.

• If given, cloud[4] is the coherent scattering length otherwise its equal 1.

• If cloud is single float the value is used as radius of a sphere with 10x10x10 grid.

Drfloat

Rotational diffusion constant in units 1/ns.

lmaxint

Maximum order of spherical bessel function. ‘auto’ -> lmax > 2pi*r.max()*q/6.

Returns:

dataArray

Columns [w; Iqwinc; Iqwcoh] Input parameters as attributes.

Notes

See transRotDiffusion() for more details. The Fourier transform of the exp function is a Lorentzian so the exp should be changed to a Lorentzian.

References

[1]

Incoherent scattering law for neutron quasi-elastic scattering in liquid crystals. Dianoux, A., Volino, F. & Hervet, H. Mol. Phys. 30, 37–41 (1975).

[2]

Effect of rotational diffusion on quasielastic light scattering from fractal colloid aggregates. Lindsay, H., Klein, R., Weitz, D., Lin, M. & Meakin, P. Phys. Rev. A 38, 2614–2626 (1988).

Examples

import jscatter as js
import numpy as np
R=2;NN=10
Drot=js.formel.Drot(R)
ql=np.r_[0.5,2:18.:3]
w=np.r_[-100:100:0.1]
grid=js.ff.superball(ql,R,p=1,nGrid=NN,returngrid=True)
p=js.grace()
iqwR1=js.dL([js.dynamic.rotDiffusion_w(w,q,grid.XYZ,Drot) for q in ql])
p.plot(iqwR1,le=f'NN={NN:.0f} q=$wavevector nm\S-1')
p.yaxis(scale='l',label=r'S(\xw\f{}) / a.u.',min=1e-4,max=1e4)
p.xaxis(label=r'\xw\f{} / ns\S-1',min=-100,max=100)
p.legend(x=30,y=9000,charsize=0.8)
# p.save(js.examples.imagepath+'/transRotDiffusion_w.jpg', size=(2,2))

jscatter.dynamic.frequencydomain.transDiff_w(w, q, D)

Translational diffusion; dynamic structure factor in w domain.

Parameters:

warray

Frequencies in 1/ns

qfloat

Wavevector in nm**-1

Dfloat

Diffusion constant in nm**2/ns

Returns:

dataArray

Notes

Equ 33 in [1]

\[I(\omega,q) = \frac{1}{\pi} \frac{Dq^2}{(Dq^2)^2 + \omega^2}\]

References

[1]

Scattering of Slow Neutrons by a Liquid Vineyard G Physical Review 1958 vol: 110 (5) pp: 999-1010

Examples

import jscatter as js
import numpy as np
ql = np.r_[0.5,2:18.:3]
w = np.r_[-100:100:0.1]
p = js.grace()
iqwD = js.dL([js.dynamic.transDiff_w(w,q,0.02) for q in ql])
p.plot(iqwD,le=f'q=$wavevector nm\S-1')

p.yaxis(scale='l',label=r'S(\xw\f{}) / a.u.',min=1e-7,max=100)
p.xaxis(label=r'\xw\f{} / ns\S-1',min=-100,max=100)
p.legend(x=30,y=100,charsize=0.8)
# p.save(js.examples.imagepath+'/transDiff_w.jpg', size=(2,2))